二叉树的遍历和判断完全二叉树

二叉树是树形结构的一个重要类型。实际问题中的许多数据都可抽象成二叉树的形式，一般的树也能用很简单的方法转换成二叉树进行存储，而二叉树的存储结构和算法都较为简单，因此，二叉树的应用十分广泛。

1.二叉树的定义

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集；可以只有一个根结点；可以只有左子树或右子树；也可以既有左子树又有右子树。

二叉树的五种基本形态如图12－7所示。

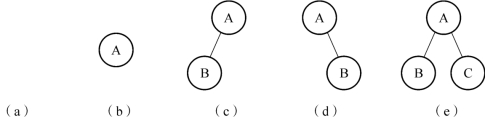
图12－7　二叉树的五种基本形态

其中，(a)为空树，(b)为只有一个根结点的树，(c)为只有左子树的二叉树，(d)为只有右子树的二叉树，(e)为既有左子树又有右子树的二叉树。

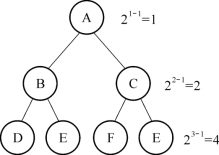
图12－8　二叉树结构图

2.二叉树性质

性质1:二叉树第i层上的结点数目最多为2i－1(i≥1)(如图12－8所示)。

性质2:深度为k的二叉树至多有2k－1个结点(k≥1)。

性质3:在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0＝n2＋1。

性质4:包含n个结点的二叉树的高度至少为log2(n＋1)。

3.不同形态二叉树

1)满二叉树

一棵深度为k且有2k－1个结点的二叉树称为满二叉树。其特点是:①每一层上的结点数都达到最大值。即对给定的深度，它是具有最多结点数的二叉树。②满二叉树中不存在度数为1的结点，满二叉树的结点的度要么为0(叶子结点)，要么为2(非叶子结点)，每个结点均有两棵高度相同的子树，且树叶都在最下一层上。

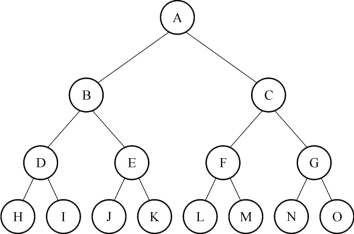
图12－9　满二叉树

图12－9是一个深度为4的满二叉树。

2)完全二叉树

若一棵二叉树至多只有最下面的两层上结点的度数小于2，并且最下一层上的叶结点都集中在该层最左边的若干位置上，这样的二叉树称为完全二叉树。特点是叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部，显然，满二叉树必定是完全二叉树，而完全二叉树不一定是满二叉树。在满二叉树的最下一层上，从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。在完全二叉树中，若某个结点没有左孩子，则它一定没有右孩子，即该结点必定是叶结点。

在图12－10中，结点C没有左孩子而有右孩子F，故它不是一棵完全二叉树。

如图12－11所示是一棵完全二叉树。

图12－10　非完全二叉树

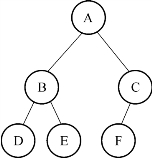
图12－11　完全二叉树

4.二叉树的遍历

所谓遍历是指沿着某条搜索路线，依次对树中每个结点做一次且仅做一次访问。访问结点所做的操作取决于具体问题的需要。遍历是二叉树最重要的运算之一，是在二叉树上进行其他运算的基础。(www.xing528.com)

1)遍历方案

从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作:访问结点本身(N)；遍历该结点的左子树(L)；遍历该结点的右子树(R)。

以上三种操作可以有6种执行次序:NLR、LNR、LRN、NRL、RNL、RLN。其中，前三种次序与后三种次序对称，故只讨论先左后右的前三种次序即可。

2)三种遍历的命名

根据访问结点操作发生位置命名:

NLR——前序遍历，访问结点的操作发生在遍历其左右子树之前。

LNR——中序遍历，访问结点的操作发生在遍历其左右子树之间。

LRN——后序遍历，访问结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node)、L(Leftsubtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又可以称为先根遍历、中根遍历和后根遍历。

3)遍历算法

中序遍历的递归算法定义——若二叉树非空，则依次执行如下操作:遍历左子树；访问根结点；遍历右子树。

前序遍历的递归算法定义——若二叉树非空，则依次执行如下操作:访问根结点；遍历左子树；遍历右子树。

后序遍历的递归算法定义——若二叉树非空，则依次执行如下操作:遍历左子树；遍历右子树；访问根结点。

例12－6　给定一棵二叉树，如图12－12所示，判断其是否为完全二叉树。

分析:根据完全二叉树的定义可知，该树不是完全二叉树，因为E的左子树为空，而其右子树不为空。所以它不符合完全二叉树的定义，因此也一定不是满二叉树了。

例12－7　给定如图12－13所示的二叉树，分别写出它们的前序、中序、后序遍历。

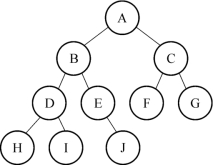
图12－12　例12－6二叉树

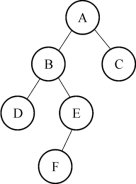
图12－13　例12－7二叉树

分析:根据三种遍历的定义，可得:(1)前序遍历为ABDEFC；(2)中序遍历为DBFEAC；(3)后序遍历为DFEBCA。

例12－8　一棵树的前序遍历为ABDECFGHI，中序遍历为DBEAFCHIG。请画出这棵树，并写出它的后序遍历。

分析:根据前序遍历的定义可知，前序序列中的第一个结点“A”是整棵树的根；在中序遍历中找到根，根左边的全部结点即是左子树的结点，根右边的全部结点即是右子树的结点。由此可画出该树的第一层结构。

之后，用同样的方法分析左子树:左子树包括D、B、E三个结点，在前序遍历中最先出现的是B，因此B是左子树的根结点；在中序遍历的左子树元素(D、B、E)中，左子树根B左边的D是B的左子树，左子树根B右边的E是B的右子树。由此可再画出该树的第二层结构中的左子树部分，如图12－14所示。

按照这样的方法进行递归分析，直到找到的每棵子树都不再有子树时，即得到整棵树的结构。最后的结果如图12－15所示。

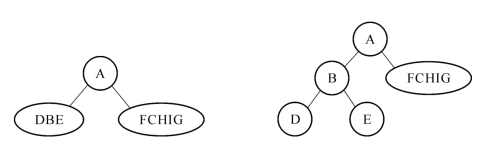
图12－14　分析例12－8树结构的过程

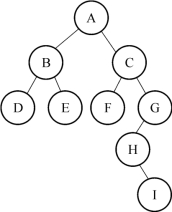
图12－15　例12－8的树结构