【摘要】：数学的统一美是指数学中部分与部分、部分与整体之间的和谐一致。前面说五凤楼从一楼到三楼再到楼顶，都是比较对称均衡的，究其根本还体现在数学的统一性上：为与五凤楼平面均衡对称相统一，楼顶的处理也比较对称均衡。由此可以看出，在建造的时候追逐统一美，才有了五凤楼和谐的对称均衡布局。
数学的统一美是指数学中部分与部分、部分与整体之间的和谐一致。对称虽说也是和谐的表现之一，但统一美在和谐上有更广泛的表现，这种美是兼顾部分与部分、部分与整体的大局意识的和谐。
不得不承认，许多数学的公式、定理都是数学家在探索出特殊例子的基础上追寻一个统一的规则或公理而诞生的，如三角形的面积公式
、等差数列前n项和公式
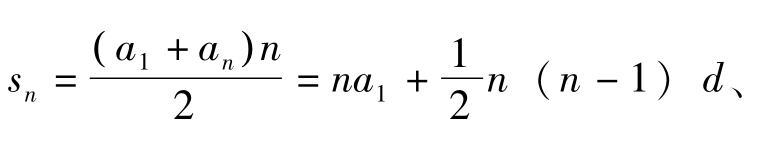欧几里得公理、皮亚诺公理……公理化方法经常被作为一个单一的方法或者一致的过程来讨论，数学的发展将日益证明数学的统一性。所有的数学家所做的工作都是进一步揭示数学本身的统一性。
纳西族的铺地图案主要由几何形图案与自然形图案组合而成，采用瓦片、鹅卵石铺设的玫瑰曲线图案，有三叶玫瑰曲线、四叶玫瑰曲线、五叶玫瑰曲线、八叶玫瑰曲线等，充分体现了纳西族人民的智慧，给人一种数学美的享受。而各种玫瑰线在数学上具有高度的统一性，可以用一个极坐标方程表示玫瑰线：ρ（θ）=asin（kθ）或ρ（θ）= acos（kθ），其中a决定玫瑰线叶子的长度，k决定玫瑰线叶子的个数和周期。(www.xing528.com)
前面说五凤楼从一楼到三楼再到楼顶，都是比较对称均衡的，究其根本还体现在数学的统一性上：为与五凤楼平面均衡对称相统一，楼顶的处理也比较对称均衡。由此可以看出，在建造的时候追逐统一美，才有了五凤楼和谐的对称均衡布局。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
