纳西族数学文化在小学教育中实践研究成果

现代纳西族民居建筑一般是两层木构楼房，高约7.5 米，也有少数三层楼房，大多为土木结构。布局形式有三坊一照壁、四合五天井、两拐房、一字排等几种形式，其中三坊一照壁是丽江纳西族民居中最基本、最常见的民居形式。可以说绝大多数农村里的农舍都是三坊一照壁的布局。

图2-22　三坊一照壁鸟瞰图

图2-23　三坊一照壁平面图

图2-24　三坊一照壁正视图

“三坊一照壁”即正房一坊，左右厢房、草楼各一坊，加上正房对面的照壁，围绕院子组合成一个封闭的三合院。正房略高于左右两坊，方向朝南，面对照壁，看上去主次分明、布局协调。屋顶深长的“出檐”、具有曲度的“面坡”，巧妙地运用数学的曲线美越过了沉重呆板的界限，一条条柔和优美的曲线形成了纳西族建筑中一道靓丽的风景线。纳西族建筑主要由正房、厢房、厦子（外廊）、天井、门楼、照壁等几个部分组成。仔细观察发现照壁、天井、门楼及悬鱼中均蕴含了丰富的数学文化。

（一）照壁中的数学文化

照壁是中国传统建筑特有的部分，具有辟邪、遮挡视线、分割建筑物等功能。纳西族民居中的照壁主要从白族民居借鉴而来。纳西族民居的照壁以三坊一照壁中正房所对的天井照壁为重点。照壁的形式多种多样，主要式样有独脚照壁（又称一滴水或一字平）和三滴水照壁。独脚照壁在实际生活中的应用没有三滴水照壁广泛，纳西族民居建筑中三滴水照壁居多，如丽江古城口大水车后面的照壁。独脚照壁墙顶平齐不分段，形制以中轴对称为基本原则，强调左右对称、统一，看起来整体高大、稳重、霸气。三滴水照壁的壁面分三段，整体是轴对称图形，中间为主壁，两边为副壁。纳西族是一个喜爱画画的民族，从下图便可看出，纳西族喜欢在照壁上画寓意深长的画。如果是三滴水照壁，一般在主壁上书写“福”“紫气东来”或“彩云南现”等大字，副壁上画画或开矩形窗户，或干脆什么都不写。由下图可见，照壁本来是矩形，4 个直角，但纳西族喜欢把照壁画成“八字墙”，即用一条线段截4个直角，形成一个等腰直角三角形，在等腰直角三角形内画装饰图纹，4条线段和原来矩形的4条边所围成的图形则变为8 个角，这种图形即八字墙。在八字墙内画画或题字都给人一种聚焦中心的感觉，重点突出。

图2-25　独脚照壁（左）和三滴水照壁（右）

图2-26　无图无字（左）和题字（右）的三滴水照壁

至于为什么三滴水照壁比独脚照壁受欢迎，那得从数学的角度来看。一般来说，整个照壁的面宽约等于院子的宽度，主壁高度约等于厢房上房檐口的高度，副壁大小相等且对称，高度与厢房下重檐间的“烽火墙”等齐。重庆大学米满宁教授等研究大理喜洲白族照壁时发现，主壁、副壁的长度与院子的宽度的尺寸存在一定的比例关系。而纳西族民居中的照壁主要是从白族民居借鉴而来，在照壁的比例上也借鉴了白族照壁：“一般把院子的宽度即照壁的总面宽，分成18 ～20份。主壁是整个照壁的中心部分，故占比也相对副壁多，一般主壁占10 ～12份，而左右两边副壁对称且宽度相等，一般占4 份。如设x =院子的宽度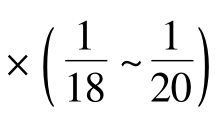 ，则一般副壁宽度为4x，主壁宽度为10x ～12x。正是组成照壁的每一部分都与院子的宽度有关，才使得整个院落看起来协调、恰到好处。”[22]

（二）天井中的数学文化

天井，俗称院落或院坝，是纳西族民居中的重要活动空间，除供生活之用外，还可以用来晒谷子或加工粮食等。由于它具有这两个功能，故农村的天井稍大。丽江地区雨水较多，大部分的雨水会积聚到院子里面，所以纳西族人民称院落是家中的风水宝地，有顺顺利利、积福纳财的寓意。纳西族的天井是纳西族人民的生活所不可或缺的。纳西族人民的院子里常栽种松树、竹子、梅树、兰花及名贵的花卉，形成了“家家有院，户户养花”的局面。正所谓“赏心乐事家家院，悦目芬艳处处花”。再加上纳西族人民能歌善舞，爱好艺术，文化素质较高，历代产生过不少知名的文人、画家、专家、学者。良好的民族文化艺术传统，加以不闭关自守，不盲目排外，善于学习和吸收其他民族的先进文化，必然对建筑艺术产生积极影响，这种建筑艺术有不少体现在天井的地面图案上。天井是丽江纳西族民居平面构图的中心，其铺地通常采用块石、瓦片、砖、鹅卵石等材料按照民间风俗习惯铺砌成具有象征意义的图案。这些手法古朴、鲜明生动的图案，涉及花鸟鱼虫、阴阳八卦、民间传说、神话故事等，如“四蝠闹寿”（如图2-27）、“鸳鸯踩莲”（如图2-28）、“鹿鹤同春”（如图2-29）、“八仙过海”（如图2-30）、“四鱼戏珠”（如图2-31）等具有观赏性同时又具有象征意义的图案，使一个普普通通的院子变得美轮美奂。

图2-27　四蝠闹寿

图2-28　鸳鸯踩莲

图2-29　鹿鹤同春

图2-30　八仙过海　

图2-31　四鱼戏珠

天井平面一般为矩形，铺砌出的图案大多数具有向心性。以纳西族地区常见的大型铺地图纹“四蝠闹寿”为例，“四蝠闹寿”也称“四蝠拜寿”“四蝠如意”“四面来蝠”，隐喻“四季皆福”。其中“四”有“四季平安”之意，“蝠”又与汉字“福”同音，有着福泽、福气、福分之意，而“四蝠闹寿”图案四周由一圈连绵不断的线条组成的工字扣纹饰构成。这一圈线条一环扣一环，纵贯相连，没有开头和结束的地方，纳西人民把它叫作“望不穿”，预示着好运连连、家中人丁兴旺、不会漏了财气与福气。传统的“四蝠闹寿”图案，是在天井地面上用瓦片和鹅卵石镶出一块正方形，并用瓦片在四个直角镶出舒展翅膀的蝙蝠。蝙蝠翅膀呈弧形，隐约可以看出四叶玫瑰的形状，正方形正中心是“寿”字的吉祥图案，寿字图案整体呈圆形，一分为四，每四分之一圆对应一只蝙蝠。整个“四蝠闹寿”图形是轴对称图形且对称轴不唯一。值得一提的是，传统汉文化里并没有“四蝠闹寿”图案，有的是“五蝠团寿”图案，其是五只蝙蝠围绕圆寿的组合纹饰。但建筑文化在交流过程中，传到边陲纳西族居住地区却作“四蝠闹寿”的构图，这种构图更严谨、均衡、对称！足见纳西族先民在接受外来文化的同时，也在思考是否符合自己本民族的文化，不是纯粹的“拿来主义者”。这种兼容并蓄的处理方式得到大部分纳西族人民的认同，故现在丽江地区的天井铺地大部分是“四蝠闹寿”的模式。“四蝠闹寿”模式不仅在天井中可见，在建筑上的装饰图也可见，甚至在花格窗上也雕刻“四蝠闹寿”纹饰。

图2-32　汉文化中的“五蝠团寿”图案

仔细观察就会发现丽江纳西族天井地面图案中蕴含着很多数学元素。以方程和图像结合的形式直观地表达出院落地面图像中所包含的数学元素，能更形象生动表达地出院落文化中的数学元素。对丽江纳西族天井地面图案中的数学问题进行研究，探析纳西族文化与数学文化的共通性，把丽江纳西族院落铺地中的数学元素挖掘出来，对纳西族的民族文化传承与传播有历史性的意义。

纳西族在铺设天井的地面时非常讲究美感，除了非常显眼的大型图案之外，还有一些用来修饰主图的小图案。各家各院的修饰图案是不一样的，这些铺地图案大致分为几何形与自然形：几何形多由直线与曲线连同三角形、四边形、多边形、圆形等组成，以这些初等几何图案为单位元素，通过旋转、平移、排列、组合等方式形成更为复杂的几何图案，再在图案中添加玫瑰曲线、心形线、螺旋线、星形线、双纽线、蝴蝶曲线等几何曲线形成一幅幅美轮美奂的几何图案。以上所说的这些曲线在数学很常见，但是应用到生活中的却是少之又少，而纳西族院楼的铺地图案则充分地把这些几何曲线运用起来了，使铺地图案尽显民族特色。自然形的图案有花草枝叶、吉祥动物、神话传说等。纳西族的铺地中主要以几何形图案与自然形图案组合而成。如采用瓦片、鹅卵石铺设的玫瑰花图案，有的是三叶玫瑰，有的是四叶玫瑰、五叶玫瑰、八叶玫瑰等等，这些充分体现了纳西族人民的智慧，给人一种数学美的享受。

1.玫瑰曲线

常言道“赠人玫瑰，手有余香”，以表达分享的乐趣。纳西族人民具有乐善好施、乐于助人的良好品质，这些良好品质与纳西族人民的生活习性和传统文化是分不开的。于是，在纳西族民居的天井铺地中就有象征着此含义的标志——玫瑰。这种形似玫瑰的图案称为玫瑰曲线（简称玫瑰线）。平面内围绕某一中心点平均分布整数个正弦花瓣的曲线称为玫瑰曲线。

玫瑰曲线的极坐标方程为：

其中a是一个固定值，代表从极点到玫瑰形最远点的距离，其决定玫瑰曲线叶子的长度；k是一个参数，决定玫瑰线叶子的个数和周期。当k =1 时，曲线ρ（θ）= asinθ是单叶玫瑰曲线，其实就是以a为直径的一个圆；当k为其他自然数时，曲线ρ（θ）= asin（kθ）所围成平面图形是玫瑰形。根据玫瑰曲线方程判断是几叶玫瑰，可以看系数k的性质：

（1）当k为整数且为奇数时，玫瑰曲线叶子的个数为k，周期为π，此时称曲线ρ（θ）= asin（kθ）为k叶玫瑰曲线；

（2）当k为整数且为偶数时，玫瑰曲线叶子的个数为2k，周期为2π，此时曲线ρ（θ）= asin（kθ）为2k叶玫瑰曲线；

（3）当k为分数时，分子B分母A均为奇数时，玫瑰曲线叶子数为B，周期为Aπ；

（4）当k为分数时，分子B分母A有一个为偶数时，玫瑰线叶子数为2B，周期为2Aπ。

以三叶玫瑰曲线方程ρ（θ） =10cos（3θ）为例，k =3 为整数且是奇数，故此玫瑰线方程通过MATLAB绘图，展现在眼前的就是三叶玫瑰曲线。

MATLAB软件程序代码如下：

close；clc；

a=10；

k=3；

theta=0：pi/100：pi；

rho=a*cos（k*theta）；

h=polar（theta，rho）；

set（h，‘color‘，［1，0，0］，‘LineWidth‘，2）。

运行该程序，得到三叶玫瑰曲线图像，如图2-33 所示，对比纳西族天井中的玫瑰图案，不得不感叹纳西族人民身边就存在着数学元素。三叶玫瑰曲线又叫三叶草曲线。数字“3”在丽江纳西族人民的生产生活中有着非常重大的意义，在丽江纳西族的神话传说中出现过一个叫“三多”的神，是纳西族人民的守护神。在纳西族人民对“三多”崇拜不亚于佛门中人对佛祖的尊敬。纳西族地面图案中的三叶玫瑰，表达了对“三多神”的尊敬。

图2-33　三叶玫瑰曲线

图2-34　天井中的三叶玫瑰图案

当k=2 时，得到四叶玫瑰曲线图像，如图2-35 所示。四叶玫瑰线曲线又叫四叶草曲线。在民间三叶草是非常常见的，但是四叶草却非常难得一见，如果谁找到了四叶草意味着得到幸运之神的眷顾。它的四片叶子分别代表着爱情、事业、荣誉、健康。由此，纳西族人民便利用这一美好象征用来装点自己的院落，一来美化了自己的居住环境，二来也表达对美好生活的一种希冀。

图2-35　四叶玫瑰曲线

图2-36　天井中的四叶玫瑰图案

当 时，得到五叶玫瑰曲线图像，如图2-37 所示。在纳西族东巴文化里，五有很多意思，第一层意思大家都知道，就是五行——金、木、水、火、土，代表着整个大自然，是构成物质的基本元素，说明世界万物的形成之间的相互关系。在这里，纳西族人民说的是铁、木、水、火、土，其意义一样，都是说明了世间万物之间的关系。它同五叶玫瑰曲线的五个花瓣有着内在联系，纳西族居住区地面上有很多这样的五叶玫瑰曲线。对纳西族而言，五叶玫瑰曲线的五个花瓣代表的是孝顺、爱情、子女、财富、平安，它体现了纳西族的整体观念和阴阳的平衡观念，描述了运动的形式和变换的关系。在纳西族地区地面图案中有很多的五叶玫瑰曲线图案，体现纳西族人民对大自然的热爱，遵循五行和阴阳平衡的准则。

图2-37　五叶玫瑰曲线

图2-38　天井中的五叶玫瑰图案

当k=7 时，得到七叶玫瑰曲线图像，如图2-39。图2-40 为七星街的纳西族民居里的地面图案，仔细观察，它有7 个相同大小的花瓣，这是七叶玫瑰曲线的函数图形。七叶玫瑰曲线与天上北斗七星对应，北斗七星由七颗明亮的恒星组成，很容易识别，被称为指向北极星的指针，可以帮助人们在夜间辨认方向。在纳西族人民看来，它为纳西族的繁荣、幸福和健康指明了方向。

图2-39　七叶玫瑰曲线

图2-40　天井中的七叶玫瑰图案

当k=4 时，得到八叶玫瑰曲线图像，如图2-41 所示。八叶玫瑰曲线中的“八”谐音“发”，有发财、发掘、发现等意思。仔细观察图2-42，它有8 个相同大小的花瓣。根据八叶玫瑰曲线的图像（如图2-41 所示），对比两图不难看出图2-42 就是八叶玫瑰曲线在天井中的图案诠释。

图2-41　八叶玫瑰曲线

图2-42　天井中的八叶玫瑰图案

当k的取值不同时，可以得到不同的玫瑰曲线，这样就出现了很多的变式，有三叶玫瑰曲线、四叶玫瑰曲线、五叶玫瑰曲线、七叶玫瑰曲线、八叶玫瑰曲线等。仔细观察纳西族天井中的图案，还有十叶玫瑰、十六叶玫瑰等，这真是个庞大的玫瑰曲线家族。由此可见，玫瑰曲线的美是无穷的，灵活性也是非常强的。在纳西族的天井图案中有很多图案属于这个玫瑰曲线家族，天井的主人用不同的玫瑰曲线表达对神灵的尊敬或对生活的美好希望。

2.星形线

纳西族是“披星戴月”的民族，勤劳、质朴、热情、好客。纳西族有“肩挑日月，背负七星”的说法，这是纳西族以勤劳为美德的象征。故纳西族东巴文化里随处可见“星星”的影子。包罗万象的建筑文化，不仅仅有自然界常见的事物，还涉及了天文地理，在天井中铺设“星星”自然合情合理。如图2-43 所示，很明显看出圆形里内嵌的是一个星形图像。星形使人联想到挂在夜空中光芒四射的星星，这一图案的构思正是来自于纳西族人民对奇特天空的奇思妙想。他们通过星星来寄托对家族未来的希望，表达家族能够熠熠生辉的美好愿望。同时图2-43 这个图案外形就是一个铜钱的形状，寓意财源滚滚。如若从数学的角度去了解、观察、分析，便发现圆内这一图案就是一个标准的星形线函数图像。

星形线（Astroid）的参数方程为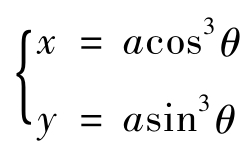：，其中θ 为参数，a C>0 o为中心到尖端的距离。星形线的直角坐标方程为：。星形线所包围的面积为。这是因为星形线是关于x轴和y轴对称的，参数θ从0 变到正好是它在第一象限部分的图像。所以：

图2-43　天井中的星形线

图2-44　星形线函数图像

图2-43 为天井中的星形线，一般纳西族都会把星形线内嵌于一个圆内，圆代表月亮，有“披星戴月”的寓意。图2-44 为星形线函数图像，以对称、均衡、抽象、明快、秩序性等的形象给我们一种数学上的美感。

星形线的弧长为6a。由以上图形可见，星形线的弧长在第一、第二、第三、第四象限里对称且均匀地分布，故只要计算第一象限部分的弧长，再乘以4 即可求出星形线的总弧长。

瑞士著名的数学家Johann Bernoulli（约翰·伯努利）是第一位对星形线进行研究的数学家。1836 年，星形线正式定名，首次出现在正式出版的图书中。星形线英文为Astroid，源于希腊文的“星星”，星形线由于有四个尖端，有时也被称为四尖内摆线，属于超椭圆的一种，几乎和椭圆的渐屈线相同。

研究发现，若让一个半径为1 的圆在一个半径为4 的圆内部，沿着圆的圆周旋转，小圆圆周上的任一点形成的轨迹即为星形线。

图2-45　星形线的轨迹

如上图所示，求解星形线的轨迹方程，设大圆O的半径为a，小圆C的半径为b。设开始点在点A处，以大圆的圆心O 为原点，x 轴方向为正方向，建立起直角坐标系，其中：，那么根据上式以及圆弧的弧长公式可得：b·∠BCM=a·θ，其中θ=∠BOA，a =4b，所以∠BCM =4θ，再过C 点做线段CD平行于x轴，则∠BCD=∠BOA=θ，从而：

接下来再根据矢量代数方法，矢量按基本矢量的分解式有：

再运用三角公式：3cosθ + cos3θ = 4 cos3θ，3sinθ- sin3θ = 4 sin3θ，得到：

则星形线的参数方程为：

亏格：若曲面中最多可画出n条闭合曲线而不将曲面分开，则称该曲面亏格为n。以实的闭曲面为例，亏格n 就是曲面上洞眼的个数，如球面没有洞，则n=1。星形线是一个几何亏格为0 的代数曲线（在代数几何中，一条代数曲线是一维的代数簇）的实数轨迹，其方程式为：

因此星形线为六次曲线，在实数平面上有四个尖瓣的奇点，分别是星形线的四个顶点，在无限远处还有两个复数的尖瓣的奇点、四个重根的复数奇点，因此星形线共有十个奇点。

3.心形线

纳西族是一个崇尚爱情的民族，当恋爱自由与婚姻不能自主而产生了不可调和的矛盾时，殉情现象便层出不穷。纳西族三大史诗故事之一的《鲁般鲁饶》就是反映殉情的经典。后来形成了颇具规模的殉情文学，这些作品经东巴祭师声情并茂地诵读咏叹，再加上民间歌手艺人的歌吟，为年轻气盛、沉醉于春花秋月中的少男少女们描绘了一个“世外爱情乐园”——“玉龙第三国”。

在玉龙雪山有两座隔不断、拆不散，遥遥相望的山，它们分别是阿老山（玉龙雪山以东，纳西人称之为“东山”的连绵山峦之中，那座高耸入云的山岭）与阿奶山（挺立在丽江坝子南面的山，又名“文笔峰”）。阿老山像倚天的宝剑，阿奶山像写天的笔头，苍黛的姿影如出自同一个模子，相似极了，就像两位古稀老人，总是那么深情地遥望着，遥望着。这其中有个凄美动人的爱情故事：

很久很久以前，有一个美丽的纳西姑娘和一个英俊的纳西小伙，他们一起在高山牧场放牧。姑娘放一群白羊，小伙放一群黑羊。每天他们让羊群合在一块自由自在地啃草。这样的幸福招来米利术恶神的嫉妒，他朝高山牧场施了个魔法，在天昏地暗的混乱中将姑娘抓走，藏在一个无人知晓的山洞里。英俊的小伙不愿失去心爱的人儿，系上姑娘送给他的洁白腰带，擦干眼泪，决定就算走到天涯海角也要找到他心爱的姑娘。他找啊找，直到青丝变成了白发，终于皇天不负有心人，他们在山洞中见面了。可当他们从洞中逃出的时候被发现了，恶神又施起魔法，将这对恩爱的人儿拆散隔远，并让他们立身化作两座高山，男的在东面，女的在西面，就是现在的阿老山和阿奶山。他们各在一方，但无论多久他们的感情都是拆不散、隔不断的，他们永远相爱，永远相望……[23]

丽江纳西族人民为了纪念和歌颂这一美丽的传说，便在自家的院落内的地上铺出心形图案，以此来表达他们对忠贞不渝的感情的向往，同时寄托对永恒爱情的追求之情。这些心形图案在数学里称为心形线。

图2-46　天井中的心形线图案

心形线，也称心脏线（Cardioid），是外摆线的一种，亦为蚶线的一种。1741年，De Castillon在Philosophical Transactions of the Royal Society上发表心形线，意为“像心脏的线”。心形线是由两个半径相同的外切圆，固定其中的一个圆（这个圆就称为“定圆”），拿另外的圆（这个圆称为“动圆”）选取一个固定的点，绕“定圆”圆周滚动一周形成的。“动圆”上的固定点所经过的轨迹，因其形状像心而得名“心形线”。

图2-47　心形线的轨迹

心形线的极坐标方程为：

水平方向：ρ = a（1- cosθ）或ρ = a（1 + cosθ）（其中a > 0）；

垂直方向：ρ = a（1- sinθ）或ρ = a（1 + sinθ）（其中a > 0）；

心形线的直角坐标方程为：

心形线的参数方程为：

心形线极坐标方程中的ρ表示曲线上的点到中心的距离，称为半径，θ 表示与水平右方向的夹角。心形线所围面积计算公式为，弧长为8a。以方程ρ = a（1 + cosθ）为例，水平方向的心形线所围成的图形分上下两边并且对称，故所围成的图形面积计算公式为：

此心形线的弧长计算公式为：

另一说，心形线来源于著名数学家笛卡尔与瑞典公主克里斯汀的一段爱情故事：在笛卡尔作为小公主克里斯汀的数学老师的那段日子里，两人彼此产生了爱慕之心，但是遭到国王的阻止，国王觉得笛卡尔配不上自己的女儿，于是强硬地拆散他们，把笛卡尔驱逐出境，永远不许他迈进自己的国家一步，还扣压了之后他写给公主的所有的信件……笛卡尔回到法国后感染了黑死病，在他临死前给公主寄出了最后一封信。这一次国王拆开信却看不懂他写的是什么。交给大臣们去看，大臣们也看不懂。请了很多数学家来看，还是看不懂。因为笛卡尔在给公主的信中只有一个短短的公式：r = a（1- sinθ）。最后国王没办法，只好把信交还给了克里斯汀。当公主看到之后立刻找出纸和笔把这个方程的图形画了出来，于是乎就看到了一颗心的形状，公主马上就明白了笛卡尔的意思，他直到死都还爱着她。

一直以来，人们以为这位用心形线传情的人就是笛卡尔。然而，据考证，笛卡尔于1649 年冬受瑞典女王克里斯蒂安（也就是上文的克里斯汀）的邀请来到了斯德哥尔摩任宫廷哲学家（不是数学家），为瑞典女王授课（女王已经登基，不是公主的身份，笛卡尔也并没有遭到驱逐）。1650 年初，迪卡尔患肺炎抱病不起，同年二月病逝于瑞典（不是在法国死于黑死病）。由此可见，故事中的数学家并非笛卡尔，要么另有其人，要么，这个故事只是美丽的谎言。

在MATLAB软件中运行如下程序代码：

close；clc；

i=-pi：0.1：pi；

x = 2. *（sin（i）- sin（2*i）. /2）；

y = 2. *（cos（i）- cos（i）. ^2）；

plot（x，y）。即可得到如下图所示的心形线：

图2-48　心形线图示

在纳西族天井的地面图案中也有这样的“心形线”函数图形（如图2-46所示）。爱心是人们对爱情的表达，寄托着纳西族人民对永恒爱情的美好期待，所以纳西族人民不仅喜爱在天井中铺设心形图，也喜爱在服饰上使用心形图案。

4.等角螺线(www.xing528.com)

图2-49　丽江古城官门口石狮

在纳西族东巴文化里有很多的标志性图案，纳西族的建筑修饰中用到了很多的等角螺线。石雕动物的毛发一般都用等角螺线来表示，如丽江古城官门口前的石狮，它的毛发几乎都雕刻为等角螺线。同样，在院落的铺地中也有等角螺线。等角螺线虽是一条简简单单的曲线，但其给人舒适、赏心愉目之感。等角螺线充分地体现了数学的曲线美，是一种奇妙的曲线、优美的曲线、生命的曲线。因此，为了增强铺地的美感，纳西族人民会在铺地图案中加入等角螺线。

平面螺旋线是以一个固定点开始向外逐圈旋绕而形成的曲线。螺旋线英文为Helix，来源于希腊文，原意是“旋卷”“缠卷”。早在2000 多年前，古希腊数学家阿基米德就对螺旋线进行了研究，等角螺线由著名数学家笛卡尔在1638 年首先描述并列出解析式，但没有获得特殊结论。1645 年，托里拆利（Torricelli）发现有关等角螺线的弧长的一项性质。雅各布·伯努利（Jacob Bernoulli）后来重新认识并研究它，取得的成果最为丰硕。他发现了等角螺线的许多特性，如等角螺线在各种适当的变换（如求等角螺线的垂足曲线、求等角螺线的渐屈线、求等角螺线的反演曲线、求等角螺线的焦线及将等角螺线以其极点为中心作伸缩变换等）之后所得的曲线仍然是全等的等角螺线，因为这些变换都可以使等角螺线再生。他十分惊叹和欣赏这种曲线的特性，故要求死后将之刻在自己的墓碑上，并附词“纵使改变，依然故我”，用以象征永生不朽。可惜不懂数学的雕刻师误将阿基米德螺线（动点每绕一圈，离开中心的距离差是相等的，也称为等速螺线）刻了上去。但这是继阿基米德之后，另一位在墓碑上表现其成果的数学家。

等角螺线，指通过几何级数增加臂的距离的螺线。设L为穿过原点的任意直线，则L与等角螺线相交的角A永远相等（故其名为等角螺线），而此值为arccot（b）。等角螺线经过放大或缩小后与原图是完全相同的，就像我们不能把角放大或缩小一样，故等角螺线是自我相似的，等角螺线的渐屈线和垂足线都是等角螺线。等角螺线、对数螺线或生长螺线是在自然界常见的螺线，如向日葵、菊的种子排列成等角螺线，蜗牛的壳像等角螺线，鹦鹉螺的外壳很接近等角螺线的形状，蜘蛛网的构造与等角螺线相似，动物的角与毛等都呈等角螺线形，昆虫以等角螺线的方式接近猎物，低气压的外观像等角螺线……

图2-50　铺地等角螺线图案

图2-51　等角螺线的图示

在极坐标系中，这个曲线可以写为：其中a为极径，辐角为，因此也叫作“对数螺线”。值得一提的是时曲线是一个圆，θ →0 时，曲线接近为一条直线。由于又可以使用黄金矩形（长宽之比为黄金分割比）来构造等角螺线，故等角螺线也称为黄金螺线。在平面上，质点围绕原点逐渐离开，相对原点的角速度恒定不变，且相对于原点的距离以等比例增长，则其轨迹为等角螺线。

图2-52　黄金矩形构造的等角螺线

在现代人的日常生活中，等角螺线被广泛应用于各个方面，如抽水机的涡轮叶片的曲面为等角螺线，抽水就均匀；轧刀的刀口弯曲成等角螺线的形状，就会按特定的角度又快又好地切割草料；建筑师们设计出现代化的螺旋式的高楼，便可使得每个房间都很明亮，采光效果达到最佳；枪膛中的膛线也是等角螺线；被称为“世界七大奇观”之一的意大利比萨斜塔的楼梯，便是294 阶的等角螺线……

5.双纽线

双纽线，也称伯努利双纽线，1694 年，雅各布·伯努利首次描述它，将这种曲线称为“Lemniscate”，在拉丁文中其原意是“悬挂的丝带”，伯努利将其作为椭圆的一种类比。我们知道椭圆是到两个定点距离之和为定值的点的轨迹，而到两个定点距离之乘积为定值的点的轨迹是卡西尼卵形线，当此定值使得轨迹经过两定点的中点时，所形成的轨迹便为伯努利双纽线。设两个定点A、B 所组成的定线段AB的长度为2a，若动点M满足MA·MB = a2，那么M的轨迹称为双纽线。故双纽线是卡西尼卵形线和正弦螺线等曲线的特殊情况。双纽线是双曲线关于圆心在双曲线中心的圆的反演图形。双纽线在数学曲线领域具有至关重要的地位，在沟通各曲线的研究上起到了重要的作用，对于伯努利双纽线的研究有助于我们更好地研究其他相关曲线，达到触类旁通的效果。伯努利双纽线在轻工业和科技方面都得到广泛而恰到好处的应用，因此，对于伯努利双纽线的研究是很有现实意义的。

在纳西族院落铺地的图案中，就有图2-53 这样的图案，就像一个横躺着的“8”，但是从几何曲线的角度去观察，发现此图就是一个双纽曲线。

图2-53　铺地中的双纽线图案　

图2-54　双纽线图示

双纽线函数图形轮廓像阿拉伯数字中的“8”。在中国，8 不仅仅是个简单的数字，人们还赋予了它更丰富的意思。比如发财之意，因为8 和汉字“发”谐音。同样，双纽线的外观像我们数学符号中的一个字符“∞”（无穷），意思就是非常多或者非常少，在数学里占有非常重要的地位。

双纽线的函数图形，不仅体现了数学美的对称、和谐、抽象、简洁、精确、统一、奇异、突变，同时也具有艺术美，是形成其他一些漂亮图案的基础单位，是许多艺术设计师设计作品的主要几何元素。通过双纽线的外延和内涵，在不变形的基础上，对双纽线函数图形进行可用图式的概括，可以创作出许多优秀的艺术作品。

双纽线是由平面直角坐标系中的以下方程定义的平面代数曲线：

在平面直角坐标系中，双纽线关于坐标原点对称，a 是任意一个定点到原点之间的距离，坐标原点是切线y = ± x 的结点和拐点。从双纽线上任何一点到给定的两点的距离之积等于两点之间距离的平方。

伯努利双纽线在极坐标中的简洁的表示为：r2 = 2a2cos2θ。

在双极坐标系，伯努利双纽线的方程为：。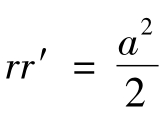

伯努利双纽线的参数方程为：

伯努利双纽线的曲率在直角坐标系中可以表示为：。正负号取决于描绘曲线时所取的方向。伯努利双纽线的曲率有一个有趣的性质：其每一点上的曲率的绝对值与此点到原点的距离成正比关系。伯努利双纽线的曲率半径计算式为：。伯努利双纽线每个回线围成的面积为a2，故伯努利双纽线r2 = 2a2cos2θ围成图形的面积为2a2。由对称性，我们可以算在第一象限内其所围成图形的面积，再乘以4 即可得到全面积。

在日常生活中，双纽线的应用十分广泛，在纺织中把伯努利双纽线作为花纹或用它编织布料等，外形美观，结构紧密，具有重复性和渐变性。伯努利本人在其《猜度术》一书中，把双纽线广泛应用到赌博中。纳西族人民除了会用伯努利双纽线铺设天井，在建筑的门窗和柱饰上也用双纽线组合或重复形成其他图形。

6.蝴蝶曲线

蝴蝶是花丛中翩翩起舞的精灵，古时蝴蝶就以身美、形美、色美、情美被人们所欣赏，被历代所歌颂。唐代大诗人杜甫就曾写过这样的诗句：“留连戏蝶时时舞，自在娇莺恰恰啼。”描绘了一幅流连忘返的春色美景。宋代出现了很多以“蝶恋花”为词牌名的千古传诵的词。喜爱美好事物的纳西族人民希望一年四季自家的院落里都春意黯然、生机勃勃，故用自己的智慧将蝴蝶留在自家的院落里，从而使院落一年四季春风常在、万花不败。而蝴蝶的外形可以用数学的方式表达出来，这种曲线称为蝴蝶曲线（Butterfly Curve）。顾名思义，蝴蝶曲线就是它的形状如同蝴蝶一样，如纳西族民居天井铺地图案（见图2-55、图2-56）。

20 世纪计算机的出现改变了数学的研究方式，以计算机为辅助工具不仅可以更有力、更方便地进行数学计算，而且可以通过计算机绘制出各种优美的曲线。使用计算机可以画出很多函数的图像，同时，通过计算机画图还能收获不少的意外惊喜。蝴蝶曲线就是其中一个意外惊喜，1989 年数学家发现了两种蝴蝶曲线。一种是一条六次平面曲线，图形和方程（Y6 = X2-X6）都很简单；另一种则通过一个特定的极坐标公式表达：。蝴蝶曲线是由美国南密西西比大学教授坎普尔·费伊（Temple H. Fay）发现的，是可用极坐标函数表示的曲线。蝴蝶曲线是一种很美的平面代数曲线，通过改变这个极坐标中的变量θ，可以得到不同形状且不同方向的蝴蝶曲线，如果再施以复杂的组合和变换，就可以构造出一幅幅精美绝伦的艺术品。自然界很多现象可以用代数曲线和超越曲线表示，蝴蝶曲线只是其中的一种，或许还有更多更复杂更美丽的曲线等待着我们去发现。

蝴蝶曲线的球坐标方程为。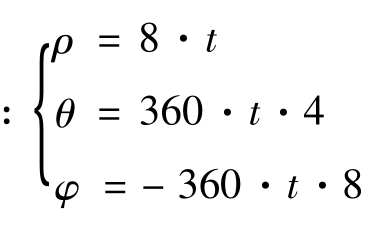

图2-55　纳西族民居天井铺地图案

图2-56　纳西族民居天井铺地图案

图2-57　蝴蝶曲线图示

7.纳西族地面图案中复杂的几何曲线

纳西族人民以柔为美，对几何图案情有独钟，在纳西族地面图案上有很多的几何图形，如矩形、三角形、梯形、圆形等基本平面图形，还有以上所讲的玫瑰线、星形线、心形线、双纽线、等角螺线、蝴蝶曲线等几何图案。经过长期积累和创造，纳西族人民将这些最基本的几何图案连接、堆积、组合成了复杂的纹样，让院落的铺地图案成为一道亮丽的风景线，如下图所示。

图2-58　其他组合的几何曲线

图2-58 的左图可以是多种图形的组合方式，可看成由1 个四叶玫瑰曲线与4 个心形线所组成的正方形，也可看成是以圆形和星形线构成的图形为基本元素，4 个这样的图形重叠在一起，中心形成1 个四叶玫瑰曲线。图2-58 中间的图是由8 个心形线等距离围绕一个圆与星形线组合而成的美丽图案。图2-58 的右图则是由六叶玫瑰曲线与十二叶玫瑰曲线重叠，堆积成一朵两层花瓣的花朵。

图2-59　组合图形

除了几何图形的组合之外，纳西族人民还将几何图形与自然图形结合或者通过自然图形的合理搭配创造出很多漂亮的图案。图2-59 所示的铺地图案为几何图形与自然图形的组合。在一块长方形的矩形中，用瓦片、白鹅卵石及黑鹅卵石便铺设出如此美丽且意义深远的图案。矩形四个角铺设圆形和星形线的组合图形，两边铺了两朵五瓣花瓣、两片叶子的小花。正中心用瓦片铺设了两个同心圆，在内圆里铺设了一条类似三角函数图像的曲线，这其实是由两个半圆的弧形拼接而成的曲线，这条曲线把内圆一分为二，左边铺满黑鹅卵石，右边铺满白鹅卵石，外圆与水平方向的矩形边相切。有人说这是一个太极图，但如果它是太极图，似乎少了两样东西：左边部分应有一个用白鹅卵石铺成的小圆，右边部分应有一个用黑鹅卵石铺成的相同大小的小圆。故这算不上一个正规的太极图，只是圆形和半径为大圆一半的两个半圆弧（开口方向相反）的图形组成的几何图形。此幅图在丽江某小学铺地中出现，其用意不是在教学生太极，而是想告诉学生，万事万物都有它黑白的两面，遇到问题不能片面地去看待，应该一分为二地看待。由此我们不得不佩服纳西族人民的“空间与几何”造诣，其数学文化博大精深，完美地彰显了数学之美。

8.丽江纳西族院落铺地图案中的数学美

以上对铺地图案中的玫瑰线、心形线、星形线、双纽线等几何曲线的研究探索，表明丽江纳西族院落铺地图案中蕴含着丰富的数学文化，具有很大的数学研究价值。这些图案除了具有丰富多彩的数学知识以外，还有着特殊的美。对这些图案进行数学的对称美与旋转美分析，对传承与发展纳西文化具有重大的意义，以下我们就一起以纳西族铺地图案为载体来感受数学的美。

（1）丽江纳西族院落铺地图案中的对称美

通常的对称美，以阴阳平衡的中心思想为核心。纳西族在地面修饰的图案中充分地运用了对称，使得数学与美学完美地结合在一起，也整体展现出数学的对称美与和谐美。

对称，包括轴对称与中心对称。研究发现，纳西族无论在建筑还是其他各方面都讲究对称，我们上面介绍的很多图形都是对称的，以“四蝠闹寿”为例，可以发现整个“四蝠闹寿”蕴含着丰富的数学元素和数学美，其整体是个中心对称图形，四个“蝠”是经过旋转得到的，每一个“蝠”都是由上一个“蝠”顺时针或者逆时针旋转90°得到的，并且单独一个“蝠”也是个轴对称图形，中间的圆形图案既是中心对称的图形，又是有2 条对称轴的轴对称图形。如图2-27 的部分和整体均展现了数学中的对称美，同时，整体又不失协调，体现了和谐美。

经过观察，我们不难看出图2-60、图2-61、图2-62、图2-63 中的图案仅有1 条对称轴，而图2-64、图2-65 中的玫瑰线与星形线都是有多条对称轴的，而且还是中心对称图形。在纳西族院落地面图案中，类似这样的图案还有很多，生活中不是缺乏美，而是缺乏发现美的眼睛。

图2-60　铺地图案　

图2-61　铺地图案　

图2-62　铺地图案

图2-63　蝙蝠　

图2-64　玫瑰线　

图2-65　星形线

以上的这些小型的纳西族地面图案，虽然小却都是完美的数学图案。这些在纳西族民居的院落里非常常见，人们用一个个小图案在细节上修饰院落的大型图案，以此来衬托出院落的整体美、和谐美。

（2）丽江纳西族院落铺地图案中的旋转美

旋转在数学中运用司空见惯，在上小学的时候我们就知道什么是旋转，例如画圆的时候，用圆规一只脚作定点，另一只脚围绕这个定点旋转一周，就可以把一个圆画出来。旋转在生活中的应用也是比较多的，如汽车的行走取决于轮子的转动，直升机的飞行也是靠螺旋桨的转动等。在纳西族的地面图案中就有很多图形是经过旋转得到的，如太阳图（图2-66、图2-67、图2-68）、玫瑰曲线（图2-69）等。仔细观察下面一些图，太阳图都是以一瓣相同的花瓣依次按相同度数围绕一个圆旋转所得的。图2-69 是在一个四叶玫瑰曲线的基础上变化而来的。在纳西族院落铺地的图案中还有很多类似的玫瑰曲线图案，如五叶玫瑰曲线、六叶玫瑰曲线等，都有一个相同点，就是它们皆是经过旋转而得来的，它们以不同的角度向不同的方向旋转，形成了纳西族独有的铺地民族文化。

图2-66　太阳图　

图2-67　太阳图　

图2-68　太阳图

图2-69　玫瑰线

9.结论与思考

通过对纳西族天井中地面图案的考察、研究、梳理，我们会发现纳西族在地面的修饰上对几何图案情有独钟，特别是四叶草曲线与星形线，甚至在公园、广场等的这些公共场合都随处可见。从数学的视野去看，纳西族人民在院落地面图案中的数学智慧，涉及了对称、旋转、相似、垂直，以及可以求出解析式的四叶草曲线、玫瑰线、星形线、心形线、螺旋线、蝴蝶曲线等。这些几何图形，不仅体现了数学美的对称、和谐、抽象、简洁、精确、统一、奇异、突变等方面，同时也具有特殊的有价值的艺术美，是形成其他一些常见的漂亮图案的基础，也是许多艺术家设计作品的主要几何元素，同时也为丽江纳西族学生学习数学提供了可用的数学素材，扩大了文化研究的范畴，传承和发扬了纳西族东巴文化。仅仅是想到的、看到的就有这么多数学元素在纳西族的文化中，而实际上纳西族人民的数学智慧远远超过我们的想象，非常值得我们去深入地学习和研究。可能有人会问，纳西族人民是按照数学知识去设计天井地面图案的，还是随便铺设恰巧成了数学图形？如果是按照数学知识去设计天井铺地面图案的，那他们是如何用数学模型去指导实践的？他们是如何根据自己已有的数学知识画出图形的？由于作者研究水平、研究时间、空间以及个人学识有限，研究还不够深入，对于这方面的问题还有待进一步研究。但至少可以肯定一点，那就是纳西族的几何意识比较强，是一个善于发现数学美的民族。

（三）门楼、牌楼中的数学文化

门楼是中国传统建筑之一，纳西族把房屋主入口的大门称门楼。在丽江纳西族地区，几乎家家户户都比较重视门楼的建造，似乎门楼象征着主人家的面子，有房屋没有门是会被人取笑的。丽江纳西族的庭院，大门显得格外重要，关上大门，便于生活、搞副业，也便于饲养家禽、牲畜。同时，大门也具有防止偷窃的功能。所以，在丽江门楼是一个值得研究的有特色的建筑部分。

通常纳西民居的大门造型不夸张，外观朴实无华，尺度近人。一般门洞宽在1.8 ～2.1米之间，高度在2.6 ～3米之间，宽与高的比例为0.6 ～0.7，基本接近黄金分割比的0.618，使整个门楼看上去有美感，与整个民居的尺度也是相协调的。门楼虽然简洁，但是纳西族人讲究门的朝向，门楼还要方便进出庭院，最好有良好的环境。门楼按形式分为有厦式门楼与无厦式门楼，通常有两种设置方式：一是设有大门及二道门，大门的门楼在一漏角天井外独立设置；二是不设二道门，门楼多附山墙或后墙而设，偏于一端，忌设正中，多朝东或南向，取“紫气东来”“彩云南现”等吉祥含意。门楼按材质分有砖拱式、木过梁平拱式及木构架式三种。砖拱式门楼多为中间高两边低的三滴水牌楼式样。木过梁平拱式门楼则是以木过梁承托外包簿砖的三滴水牌楼。木构架式门楼多为双坡屋面，檐下用多层花板、花罩装饰。不仅民居建筑注重门楼的建造，一些单位（如中小学学校）的大门也建造成具有纳西族风格的三滴水牌楼式样门楼。[24]

图2-70　民居门楼和学校门楼

门楼以砖木修饰为主，有拱圈式和雀台式两种构造，青砖灰瓦，绘上山水花鸟画或题上古诗词。有的在大门上写有“集祥、凝瑞”或福禄寿禧等字样。门槛前有两个石方块，与门楼栋梁上的两个木块相对应，意指“门当户对”。这是纳西族先民以陆神石代表门神的民俗习惯。

门楼的设计精美程度因其主人的重视程度不同而有所区别。一般平民老百姓家中的门楼均为无厦式门楼，多用砖雕、泥塑、镶砖手法修建和装饰，门顶一面厦出水，即普通的坡屋面式，设计简单，尺寸也比较合理；但是富裕家庭、享有盛名的公园或一个古镇的门楼设计就比较精美繁复了。如图2-71 所示，黑龙潭公园和束河古镇的门楼，建筑尺寸在宽度及高度上都比一般民居建筑的门楼显得“霸气”，而且在门楼的顶部有两层翘起的翼角，檐下有斗拱装饰，极为华丽。斗拱装饰或为木质，或为泥塑，气势雄伟壮丽。木质斗拱端头的跳头多雕成龙、凤、兔、象、花卉等图案，斗碗雕成八宝莲花，外饰彩色油漆或用木质本色，突出雕刻艺术的精妙。若用彩色贴金油漆装饰，则显得更加富丽辉煌。

图2-71　黑龙潭公园及束河古镇的门楼

纳西族除了讲究门楼的设计外，对牌楼的设计也是挺讲究的。牌坊，又名牌楼，为门洞式纪念性建筑物，是中华特色建筑文化形式之一，是封建社会为表彰功勋、科第、德政以及忠孝节义所建的建筑物。也有一些宫观寺庙以牌坊作为山门的，还有的是用来标明地名的。牌坊是古代官方的称呼，老百姓俗称它为牌楼。现代城市建设中牌坊则多被作为传统特色的标志物，建于风景区或街区等入口位置。其中粗制滥造、比例失调者众多，但也不乏精美壮观的成功之作。如丽江最繁华的街道七星街的牌楼及丽江“最官方”“最权威”的牌楼——木府忠义坊。由图2-72 可知，七星街牌楼及忠义坊均为三滴水牌楼，足见纳西族对数字3 的崇拜和喜爱。所不同的是，七星街牌楼是民间建筑，故设计简单，而忠义坊位于丽江的“紫禁城”木府，土司府门前，故设计独特，精美绝伦，高大霸气。一般华丽的门楼只有一层斗拱，但忠义坊有两层斗拱，均为十字斗拱，整整齐齐地排列在门梁上，门梁上的四只石狮与牌楼前的四只石狮对应，且绘饰有龙图腾。民间牌楼与官家牌楼自然是不可相提并论的，由此也可见，牌楼可以表明主人身份的高低贵贱，这和纳西族封建社会的阶级划分是密不可分的。

图2-72　七星街牌楼与忠义坊

（四）悬鱼中的数学文化

悬鱼，并非可以食用的一种鱼，而是中国古建筑上一颗耀眼的明珠。在丽江纳西族地区，无论平民百姓家还是官宦人家，从古建筑到钢筋混凝土的现代高楼大厦，都安装有悬鱼。悬鱼是建筑的一个装饰物，大多用木板雕刻而成，是最后安装的屋顶木构件（现代建筑中也有泥塑、交趾陶或剪黏的悬鱼），是丽江纳西族传统木构架建筑屋顶山面不可或缺的木构件，安装在悬山屋顶侧面搏风板的接缝处。由于其最初为鱼形，并在山面顶端悬垂，所以称为悬鱼，也称垂鱼。有的还在搏风板的两边对称排列着小三角形的云纹装饰，称为惹草。

图2-73　悬鱼

关于悬鱼，有这么一个千古传颂的成语故事——羊续悬鱼。[25]羊续（142—189 年），字兴祖，今山东邹城市石墙镇羊续村人，东汉官员，先后任庐江、南阳太守。其任南阳太守时，洁身自好，廉洁自律，拒收贿赂，哪怕只是一条鱼。

“羊续悬鱼”的故事是这样的：羊续奉命平定了南阳（今河南南阳）一带的贼寇，然后任南阳太守。羊续为人俭朴，廉洁自守，上任后很少回家探亲，他夫人便带儿子从老家千里迢迢来南阳，却被他拒之门外。羊续为官清廉，身边只有几件布衾和短衣以及数斛麦，无法招待妻儿，因此他劝说夫人和儿子返回故里，自食其力。南阳一带物产丰富，那里的官员和富人过着奢侈的生活，处处可见奢靡之风。他身为一方之守，下决心改变南阳的不良风气。一天，有府丞（府中的佐吏，即辅助太守办事的官员）给羊续送来一条当地有名的特产——白河鲤鱼。羊续自然拒收，推让再三，但这位府丞执意要太守收下。这位府丞走后，羊续只好让仆人将这条大鲤鱼挂在屋外的柱子上，任其风吹日晒，成为鱼干。没多久，这位府丞又送来一条更大的白河鲤鱼。羊续便把他带到屋外的柱子前，指着柱上悬挂的鱼干说：“你上次送的鱼还挂着，已成了鱼干，请你一起都拿回去吧。”这位府丞羞愧至极，悄悄地把鱼取走了。羊续以此杜绝了馈赠，从此就没人敢给他送礼了。当地百姓知道这件事以后，尊称羊续为“悬鱼太守”，无不称赞羊续的高风亮节。后来，文人骚客便在诗词中以“悬鱼”喻指官吏廉洁、拒收贿赂。如北宋诗人徐积的《和路朝奉新居十五首》之六：“爱士主人新置榻，清身太守旧悬鱼。”明朝民族英雄于谦有感此事曾赋诗曰：“剩喜门前无贺客，绝胜厨传有悬鱼。清风一枕南窗下，闲阅床头几卷书。”清朝聊斋先生蒲松龄的《官吏听许财物》：“不见裴宽瘗鹿，且看羊续悬鱼。”

至今此事仍以“悬鱼”“羊续悬鱼”“羊续悬枯（指死鱼）”“挂府丞鱼”等被世人广为传诵。

纳西族建筑上的悬鱼功能有四种：一是对屋顶的横梁起到保护作用；二是防水功能，丽江的夏天几乎是雨水季节，悬挂的檀条、挂枋端头的瓦纹截面因飘雨会受潮腐蚀，故使用宽大的搏风板将其隔离，悬鱼钉在搏风板中央，起到防水的作用；三是装饰功能，在悬鱼上略加修饰，绘上红、黄、蓝、绿彩绘，丰富的色彩增加了建筑物的艺术气息；四是美好期盼的功能，东巴文化里鱼寓意年年有余，且鱼生于水中，纳西族建筑多为木构建筑，故特别怕火，水能灭火，悬鱼表达了纳西族人民防火的意愿。

纳西族民居的悬鱼文化博大精深，走遍丽江会发现几百种式样，式样因民居等级、性质、规模和质量的不同而不同，长度大概在80 ～100 厘米之间，基本形式为直线形和弧线形，也有直线、弧线及多边形结合的形式。

悬鱼造型具体分两种类型。第一种是具象自然形，即鱼的造型。其可以是一整条鱼，或者只是雕刻鱼尾的形状，也可以雕两条尾部相交或不相交的鱼，呈对称图形，双鱼造型的悬鱼比较常见的就是对称式。[26]

图2-74　建筑中的悬鱼　

图2-75　建筑中的悬鱼

图2-76　建筑中的悬鱼　

图2-77　建筑中的悬鱼

由上图可知，鱼形悬鱼一眼望去便可看出鱼的轮廓。图2-74 是一只有头有尾的呈左右对称的鱼。而有的地方只是为了取其寓意，省去雕刻鱼形的繁复程序，故只雕刻鱼尾的形状，图2-75 即是如此。图2-76 的双鱼造型比较简单，雕两条尾部相交的鱼，呈轴对称图形，这种样式是比较常见的悬鱼，只不过在鱼的形态上有所变化。图2-77 的双鱼造型较图2-76 繁复一些，木板中部两边水平伸出一个像鱼鳍一样的结构，下方雕刻一朵含苞待放的莲花，仿佛吸引来了两条尾部不相交的全等的鱼，正在静静地闻花香。整个悬鱼造型是轴对称图形，鱼儿雕刻得活灵活现。“鱼”音同“余”，取余裕的吉祥之意，造型配以莲花，取“年年有余”的寓意，表达了纳西族人民对生活的美好希望。以上图中的悬鱼在古老建筑物上还保留木板雕刻的传统习惯，现代建筑的悬鱼几乎都采用泥塑的构造手法。

图2-78　美丽的悬鱼图案

讲究一点的悬鱼，除了造型上和直线、弧线等结合组合成复杂的图形外，还在木板上雕刻花纹。图2-78 的左图，悬鱼上端为直线，线至中点即刻变为曲线，且是一个周期的三角函数曲线，左右曲线对称，紧接着下方出现一个半圆弧，配上雕刻的花纹，这两个半圆弧是阿基米德螺线的一部分，最下方是两条相濡以沫、左右对称的鱼形。图2-78 的右图造型优美，曲线感浓烈，悬鱼上端为直线，线至中点即向内抠去一个小小的三角形，木板打磨得有些弧度，看起来极富美感。再往下连续截去了两个半圆，形成两个开口向外的半圆弧，最下方是两条首尾衔接、左右对称的鱼形。当然，除了上图的造型以外，还有很多形状各异、想法奇特的悬鱼造型。悬鱼是纳西族民居建筑上的一颗璀璨明珠，处处体现着纳西族人民使用几何图形创造美好事物的能力。

第二种是抽象几何形，即非鱼形。抽象类悬鱼大多抽象为几何形或近似某个造型的几何化的图形。造型上既有对称式，又有均衡式（即依中轴线或中心点组成异形的拥有上下左右结构的纹样），还有立体式（如丽江白沙乡新善行政村玉龙三社，对称式的金鱼在与鱼身平面垂直的方向上伸出一个像鱼鳍一样的结构）。图2-79 为丽江市古城区祥和商业广场的建筑物上的悬鱼，一改平日里以鱼形为造型的形象，左图既是对称式，又是均衡式，还是立体式的几何形组合。说它是对称式，因为此悬鱼虽然有多层次的图案，但左右是呈轴对称的。说它是均衡式，因为悬鱼上下共五层图案，虽然都是六边形，但以第三层的六边形为中心点，组成异形的上下左右六边形纹样。这个六边形又像化学里的苯环，每个角为120°，对称使得它更稳定，寓意丽江的商业稳定发展。右图为左右对称的工字扣图案，工字扣图案看起来庄严繁重，其实只是很简单的“一笔画”，线条大部分只能水平或垂直移动。

图2-79　祥和商业广场的悬鱼

笔者在丽江市七河镇的一户农家乐里，发现了如图2-80 所示的悬鱼。如果用一个正方形表示单位1，其边长记为a，那么整个悬鱼宽5 个正方形的边长即5a。悬鱼上方为直线，线延伸到木板中点处，随即由两边水平向内各自截取线段a，再由两边垂直向下各自截取线段a，再由两边水平向内各自截取线段a，此时，木板两边截取出“z”字形，左边呈正“z”字，右边呈反“z”字，左右两边对称，此时木板还剩下a长度的宽。由宽5a骤变为宽a，体现了数学里的突变美。随后以宽a向下延伸，到一定长度再由两边水平向外各自延伸线段a，再由两边垂直向下各自延伸线段a，再由两边水平向外各自延伸线段a，由此延伸出“z”字形，再重复截取“z”字形的程序，使得最后只剩下一个单位1 的正方形。形成的图案如图2-80 的右图所示，就像一个正方形和它的水平、垂直方向的两条对称轴所形成的。我们把最下方的图形截取下来，发现小正方形的个数呈等差对称数列（1，3，5，3，1），且水平和垂直方向同圈内的小正方形个数一致。其实，不用画出图形就可以算出图中用了多少小正方形以及右图的面积：

图2-80　几何造型的悬鱼图

在这里用等差数列的公式计算显得有些多余，但如果对复杂一点的图形却是最好不过的方法了。由等差数列前n项和公式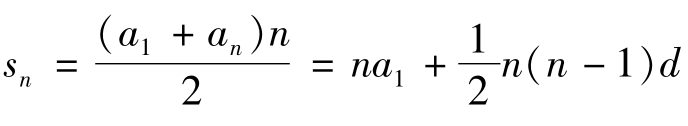，可知图2-80 的右图为对称的等差数列，共用中间项，计算时可以看作两个等差数列（1，3，5）的和减去中间项，故这种图形的计算公式为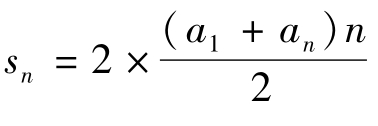-an = na1 +（n-1）an。带入计算得到的结果与之前的计算结果一致。sn = na1 +（n-1）an = 3 ×1 +（3-1）×5 = 13（个）。

这里的等差数列不是传统意义上的等差数列。它是由两个完全相同的等差数列左右逼近依次排列，共用中间项且关于中间项对称的数列，数学上称其为等差对称数列。等差对称数列可分为递增式等差对称数列和递减式等差对称数列。

数列按其对称性来分，可分为对称数列和非对称数列，通常见到的数列都是非对称数列，那什么是对称数列呢？一般地，如果一个数列第一项和最后一项是同一个数，且关于该数列中项对称，就把这样的数列叫对称数列。如：1，2，3，4，…，998，999，1000，999，998，…，4，3，2，1。对称数列分为等差对称数列和等比对称数列。如果一个对称数列从第2 项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫作等差对称数列，这个常数叫作等差对称数列的公差，公差通常用字母d 表示。如：1，3，5，7，…，97，99，97，…7，5，3，1。等差对称数列是特殊的对称数列，但其通项及前m项和皆有规律可循。一般这种数列有2n +1 项，第1 项与第2n + 1 项相同，第2 项与第2n 项相同，……，第m项与第2n +2- m项相同，中间项为第n +1 项。

故等差对称数列的通项公式为：

前m项和公式为：

其中当n +1 ≤m ≤2n时，前m项和公式为：

等差对称数列在高考题中出现过，一改等差数列的常规背景，在等差数列的基础上加上对称，似乎学生没有学过，给人以考题超纲的感觉。但是对称和等差数列都是学生再熟悉不过的数学知识，两者一结合便产生出新的数学知识，认真分析其实也不难。在纳西族的建筑装饰中经常会遇见等差对称数列的模型，足见纳西族人民已经意识到这种等差对称数列的美。

图2-81　建筑装饰中等差对称数列

图2-81 为纳西族建筑上的装饰图案，其不是彩绘的立体画，而是按照一定的规律依次挖取一个个大小相同的小正方体所形成的立体图案，最后涂上彩色。左图水平方向上依次挖取了1，2，3，4，5，4，3，2，1 个小正方体，构成等差对称数列。右图也同样构成了一个同样的等差对称数列。所不同的是，如果你仔细观察两图，右图关于垂直方向的中项左右对称，而左图不仅关于垂直方向的中项左右对称，还关于水平方向的中项上下对称，按上下方位看，依次挖取1，3，5，7，9，7，5，3，1 个小正方体，也构成等差对称数列。