博物馆与学校合作机制的影响因素分析

由上文可知，和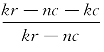是影响博物馆与学校合作意愿的最重要的两个关键节点，因而我们可以通过下述函数的增减引理，继续分析两个函数项中四个因素k，n，r，c对函数大小贡献的变化。

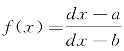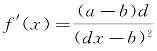（a）对于函数，因为，故而当a＜b时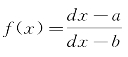为减函数，当a＞b时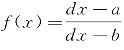，为增函数。

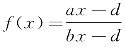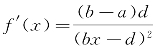（b）对于函数，因为，故而当a＜b时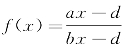，为增函数，当a＞b时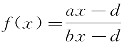，为减函数。

博物馆在馆校合作中的投入规模（k）。根据a＜b时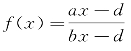，为增函数，我们可以得知，随着博物馆投入规模（k）的增加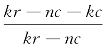，也会增大。根据a＞b时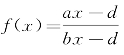，为减函数，我们可以得知，随着博物馆投入规模（k）的增加，也会变小。表示随着博物馆在馆校合作中整体投入规模的增大，相位图24中第四部分的面积和相位图22中第一部分的面积也会相应增大；而相位图24中第二部分的面积和相位图23中第一部分的面积会相应减小，复制动态系统会逐渐倾向于（1，0），远离（0，1）。这说明在馆校合作中，博物馆投入规模的增大，会使得博物馆单独负担馆校合作成本的可能性增加，而学校投入的可能性降低，搭便车的可能性增大。(www.xing528.com)

学校在馆校合作中的投入规模（n）。根据a＞b时，为减函数，我们可以得知，随着学校投入规模（n）的增加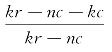，会变小。根据a＜b时，为增函数，我们可以得知，随着博物馆投入规模（n）的增加，也会增大。表示随着学校在馆校合作中整体投入规模的增大，相位图24中第一部分的面积和相位图22中第二部分的面积会相应增大；而相位图24中第四部分的面积和相位图23中第二部分的面积会相应减小，复制动态系统会逐渐倾向于（0，1），远离（1，0）。这说明在馆校合作中，学校投入规模的增大，会使得学校单独负担馆校合作成本的可能性增加，而博物馆投入的可能性降低，搭便车的可能性增大。

单位收益（r）。由于a＞b时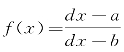，为增函数，这意味着无论还是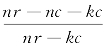都倾向于在r增加的条件下增加。这说明，在馆校合作收益增加的情况下，馆校合作虽然会演化为（0，1）或者（1，0）状态，亦即一方承担成本，一方搭便车，但是由于存在超额的利益，馆校合作可以在一方承担主要成本的状态下，保持稳定的合作。

单位成本（c）。在a＞b的状况下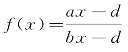，为减函数，因而随着单位成本的增加，无论还是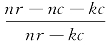都倾向于在c增加的条件下减小，博物馆与学校进行馆校合作的意愿降低，最终可能出现相位图21所描述的状况，馆校合作趋于形式化或者走向解体。