套利定价模型：性质与应用

性质1　一个充分分散化的组合，公司层面的个体风险可以被分散掉。

性质2　如果两个充分分散化的组合具有相同因素敏感度，那么在市场均衡时，它们一定具有相同的期望收益。

性质1很好理解，在之前的章节中已经证明过。性质2是说充分分散化的组合是没有非系统风险的，那么对应的均衡期望收益率是和其承担的系统风险相对应的。而系统风险是由其因素敏感度决定的，所以因素敏感度相同的两个组合一定具有相同的期望收益，否则将存在无风险套利机会，通过套利使二者期望收益相等。

根据单因素APT的式子：

其中是因素的收益率。当因素组合的风险溢价给定的时候，如果敏感度b相同，那么资产的期望收益率也一定相同。

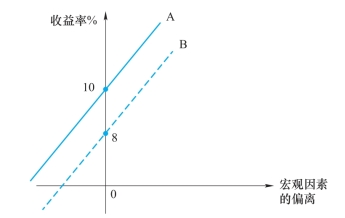
图6-2　证券A和B的收益率和宏观因素偏离图

例子：图6-2坐标系是收益率和因素对宏观因素偏离值的坐标系。

实线描绘了在不同的系统风险下，一个因素敏感度　bA=1的充分分散化的资产组合A的情况。A的期望收益率为10％。

虚线代表另一充分分散化资产组合B的收益，其收益率为8％，且因素敏感度bB也等于1。那么市场均衡的时候，组合A和B是否能够在图中的条件下共存呢？

根据性质2，如果两个组合的因素敏感度相同，当市场均衡的时候，它们的均衡期望收益率应该也相同。可见，图中A和B，它们的特征线的斜率相同，说明它们的因素敏感度相同，所以在均衡时它们的期望收益率也应该相同。

此时，可以构建套利组合，卖空组合B的同时买入等资金量的组合A，这样可以获得10％-8％，也就是2％的套利收益率。

随着套利者不断卖出组合B，组合B的价格下降，收益率上升。而随着套利者不断买入组合A，组合A的价格上升，收益率下降。直到它们期望收益率相等，套利机会消失，就满足单因素APT模型了。

性质3　对任意的两个充分分散化的投资组合i和j，它们具有不同的因素敏感度，当市场均衡时，它们的风险溢价必须正比于它们各自的因素敏感度。可表述为下式：

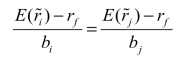(www.xing528.com)

同样，根据单因素APT的表达式：

而市场中，因素的因素组合风险溢价E（）−rf是给定的，所以均衡时任意资产风险和其敏感度的比值就是一个常数了，即之前所提的λ。因此，性质3成立。

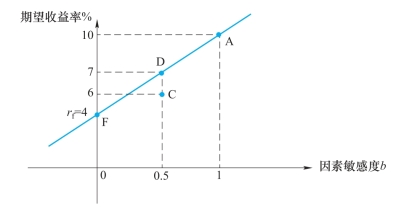
图6-3　证券的期望收益率和因素敏感度

例子：图6-3的坐标系是期望收益和因素敏感度坐标系。给定充分分散化的组合A的期望收益率是10％，敏感度是1；无风险收益率是4％；充分分散化的组合C的期望收益是6％，敏感度是0.5。

问：当市场均衡时，组合C是否存在？

根据性质3，当市场均衡的时候，充分分散化的组合的风险溢价和其因素敏感度的比值为常数。可以计算组合A和C的这个比值，组合A：（10％-4％）/1=6％；组合C：（6％-4％）/0.5=4％，两者不同，则存在套利机会。

可以利用组合A和无风险资产构造一个和C的敏感度一样，但却有着不同期望收益率的组合D。例如，组合D由50％的A和50％的无风险资产F构成，那么组合D的敏感度是0.5×1+0.5×0=0.5，组合D的期望收益为0.5×10％+0.5×4％=7％。

可以卖空组合C，同时用卖空组合C得到的资金买入组合D，相当于用资金的一半买入组合A，另一半买入无风险资产F。因此，可以得到7％-6％的无风险套利收益率1％。

性质4　对绝大多数资产i,j，其风险溢价与b值成比例：

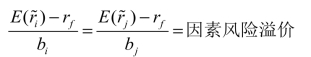
性质5　对于任意单个资产i，成立性质4，则对任意投资组合p，也成立：

性质2和性质3适用于单因素模型。

性质1-3都假设了组合是充分分散化且没有非系统风险的组合，所以用套利组合无解的方法可以证明出精确的均衡期望收益。而当组合并未进行充分分散化且存在非系统风险时，可以证明绝大多数资产的均衡收益率是符合APT的，只有有限个资产不符合。这是研究并非充分分散化的资产的渐进套利定价模型的结论。