套利定价模型证明：多因素模型

本节介绍基于多因素模型的套利定价模型的另一种推导，这种推导更加形象易懂。

市场均衡的时候，最直观的一个结论就是构建不出套利组合。即试图构造套利组合的不等式组是无解的，或市场均衡的时候，套利组合不等式组的最后一个式子不是大于零的，而是等于零的。

假设如下几个列向量，分别定义I为n维单位列向量，w为n维权重向量，bk为n维敏感度列向量（k=1,2,…,K），e为n维期望收益列向量：

根据期初无投入，不承担风险，组合期望收益率一定为零，可以列出不存在套利机会的方程组：

根据期初无投入、自融资的条件，可以列出w1+w2+…+wn=0（IT·w=0）。根据不承担第一个因素风险，可以列出b1T·w=0，还可以列出K个敏感度为0的式子。根据无套利组合的期望收益为零，列出最后一个式子：eTw=0。

由于两个向量相乘的内积等于零，意味着这两个向量是互相垂直的，则单位向量I、K个敏感度向量（b1,…，bK），以及期望收益率向量e都和权重向量w是垂直的。

如果几个向量都和同一个向量垂直，那么这几个向量之间可以互相线性表出。

图6-1　向量空间示意图

在向量空间中，如果向量I、b正交于w，蕴含着e正交与w，则e必须落在由I和b张成的二维空间上，e可以由I、b线性表出。如果e用I，b1到bK线性表出的话，可以列出下面的式子：

e=λ0I＋λ1b1+λ2b2+…+λKbK

将这个式子的列向量展开：(www.xing528.com)

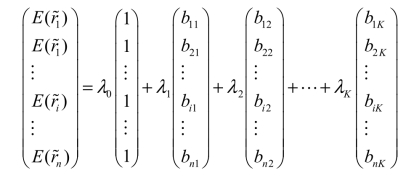
取其中的第i行，可以得到基于多因素模型的套利定价模型（APT）：

同样可以假设i为无风险资产，则：

可以假设i为某个因素的因素组合，则：

所以λk为因素k的因素风险溢价。

APT的另一种证明，需要用到Farkas引理。

根据Farkas引理，不等式组ATw≤0无解

可将w看成投资比例权重向量，由单位向量和n种风险资产对K种因素的因素敏感度

矩阵b组成的矩阵　[Ib]T看成AT，e看成期望收益率，则不等式组以及等价条件为：

同样，可以将[Ib]　λ=e中的第i行取出，即为基于多因素模型的套利定价模型（APT）。