套利定价模型证明-基于多因素模型的投资学

本节将考虑更一般的情况，即包含多个因素且存在公司个体风险的情况。假设有K个影响资产收益率的因素，市场中存在n种风险资产，每种资产的收益率都同时受到K个因素的共同影响，还假设资产的数量远远比因素的数量多(n＞K)。任意一种资产i的收益率可以用多因素模型来表示：

其中，i=1,2,…,n;k=1,2,…,K

这个多因素模型中的（1）式，也是因素对其期望值偏离的形式，因此，。同时还假设资产的个体风险的期望值为0，则。

还假设因素方差为1，公司层面的个体风险方差相等且有界，即

再假设任意两个因素之间、任意两个证券的公司个体风险之间，以及任意因素和个体风险之间都是相互独立的，有：

考虑组合p，是由n种风险资产形成的，组合中资产i的权重为wi，　Σwi=1，则rp等于n种风险资产收益率的加权和。将资产i的多因素模型代入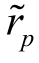中，得到：

可通过选择n种风险资产的权重，使得组合p不承担任何系统风险，要求组合p对每一种因素的敏感度为零。针对K个风险因素，得到K个关于风险的等式：

第一个等式，是组合p对因素1的敏感度，等于组合p中n种风险资产对因素1敏感度的加权和。其中bi1,i　=1…n敏感度b的第一个脚标代表第i个资产，第二个脚标代表对哪一个因素的敏感度。

同理，这K个式子表示组合p对每一种因素的敏感度都等于0，因此组合p不承担任何因素风险，就是不承担任何系统风险。

这个方程组中，有n个未知数wi，有K个方程，当n＞K时，这个方程组有解且解不止一个。可以将解出的权重代回rp的式子中，由于该组合是对所有K个因素的敏感度均为零的组合，得到：

可知组合p0的方差中没有系统风险，全部都是非系统风险。由于假设所有公司个体层面的方差都是　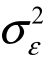，即　，所以组合　rp0的方差为：(www.xing528.com)

当资产的数量n→∞，每个资产的权重非常小，，得到：

由于假设了公司个体层面的方差有界，因此当n趋向于无穷大时，组合p0的方差趋向于零：

则市场均衡时，由于组合p0不承担任何系统风险，同时其非系统风险趋于零，因此其收益率应为无风险收益率：

（3）式中的wi是解上面的K个因素敏感度为零的方程组（2）的解，所以wi是各个敏感度b的函数。

因此，由（3）式可知，可以把各个资产的期望收益率()E r表示成无风险利率与敏感度的函数。可以证明，各种资产的期望收益率可以表示为：

i

同样可以假设资产i为某个因素k的因素组合（该组织只对因素k的敏感度为1，对其他因素的敏感度为零）时，该资产的期望收益率为，代入（4）得：

因此，λk为因素k的风险溢价。将λk代入（4）式得到基于多因素模型的套利定价模型：

可见当市场均衡无套利机会时，资产的均衡收益率等于时间价值带来的无风险收益率rf，以及因承担K种因素风险而得到的K种因素带来的风险溢价：

从形式上看，基于多因素模型的套利定价模型是多元线性的形式，非常简单和易于理解。当市场均衡时，没有任何套利机会，资产的风险溢价只能来自K种风险因素带来的风险溢价，某个因素k带来的风险溢价取决于该因素k本身的风险溢价，以及该资产或组合对因素k的因素敏感度，如果因素敏感度比较大，则承担了更多来自因素k的风险，从而要求更高的来自因素k的风险溢价。