投资学：套利定价模型的单因素应用

本节将基于单因素模型假设证明套利定价理论。

当市场达到均衡的时候，市场上是没有套利机会的，这时各资产的期望收益率会满足APT套利定价模型。

假设只有一个因素，单因素模型可以写成：

对（1）式两边同时求期望得到（2）式：

再用（2）式减去（1）式得到（3）式：

再把（3）式中的挪到右边，得到下面的（4）式：

所以单因素模型还可以写成（4）式——因素对期望值偏离的形式。

（4）式中，如果把因素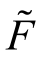看成　形式（因子偏离其期望的形式，或因子意外变动的形式）的话，那么，且（4）式可以进一步写成：

假设所有资产的个体风险都为0，即考虑没有非系统风险的资产，则资产的收益率可以写成：

其中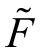，是风险因素，是宏观因素对其期望偏离的形式。因此，

假设有两种风险资产有不等于0且不相同的因素敏感度，即bi不等于bj。因此可以构造组合p，把单位化为1的总财富分配到两种风险资产上。组合中包含w比例的资产i和1−w比例的资产j，于是组合p的随机收益为：

将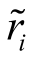和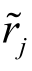的单因素模型代入上式，得：

由于有两种资产，而不确定性因素的来源只有一个，所以可以通过选择组合权重w来消除组合的不确定性，这样就能够使组合收益率E（rp)=rf。

使得组合系统风险为零的权重记为w0，有：

将w0代回rp的表达式（5）中，得到因素敏感度为0的组合p0的收益率。(www.xing528.com)

由于单因素模型的形式：

则，对因素敏感度为0的组合p0的收益率为：

当市场均衡的时候，对因素敏感度为零的组合收益率一定是无风险收益率，否则会出现套利机会。

将w0的（6）式代入得：

因此，对任意资产i的期望收益率满足：

当资产i的因素敏感度为1时，根据（7）式，资产i的期望收益率为因素的期望收益率：

可知，λ为因素的风险溢价。将λ带入（7）式，得到基于单因素模型的套利定价模型：

因此，当市场不存在套利机会时，任意资产的期望收益率满足基于单因素模型的套利定价模型（9）。且资产的均衡期望收益率和CAPM一样，由两部分组成：时间价值带来的无风险收益率rf和因素风险带来的风险溢价

在求λ时，假设某资产的因素敏感度为1，称因素敏感度为1的组合为因素组合（Factor Portfolio）。存在多个因素时，因素组合的定义为对其中某一个因素的敏感度为1，对其他因素的敏感度为零的充分分散化的组合。因此，因素组合的收益率为因素期望收益率。（8）式中的λ叫做因素溢价（Factor Premium），且因素组合没有非系统风险，只有系统风险，其系统风险就是某个因素的风险。

从形式上看，套利定价模型和资本资产定价模型差不多，都是单因素的线性模型，但两者的推出逻辑和含义并不一样。

套利定价模型和资本资产定价模型的区别与联系：

1.从推出逻辑上看，资本资产定价模型基于的是供需均衡，而套利定价模型基于的是无套利均衡，只是要求市场中不存在套利的机会。

2.在资本资产定价模型中，需要市场组合的存在为前提，市场组合的风险是整个市场唯一的风险来源，市场组合包含了所有风险资产的组合。而在单因素APT中，因素组合并没有明确指出哪个因素，也没有具体的经济含义。与其说这是套利定价模型的局限性，不如说这是套利定价模型的灵活性所在。