同单因素模型一样，在双因素模型中，一个组合对某一宏观因素的敏感性是组合中各个资产对这个宏观因素敏感度的加权平均，权重为各个资产的投资比例。
假设有这样一个双因素模型，两个因素分别为GDP增长率和通货膨胀率，
。在表5-1的基础上加入了十年的通货膨胀率数据，见表5-2。
表5-2 某证券各年收益率和GDP增长率及通货膨胀率
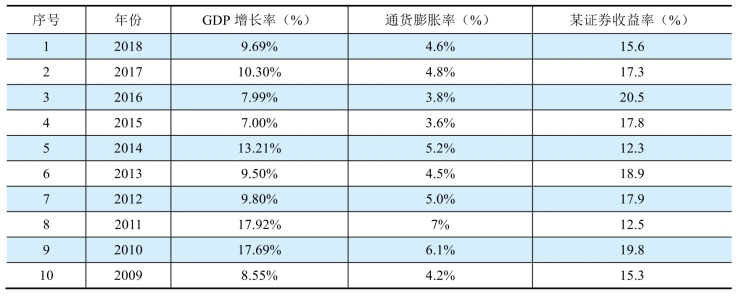
将表5-2的这十个时间点的数据描在图5-2的三维坐标系中，就是十个点。
这个三维坐标系的三个坐标分别表示GDP增长率、通货膨胀率和股票的收益率，其中纵轴是股票的收益率。
用十年的数据可以回归出该双因素模型的形式（当然现实中回归的样本数据会更多，此处只是简化举例）：(www.xing528.com)
股票A的收益率受GDP的增长率和通货膨胀率预期值的影响。图5-2中的每一点描述了在特定的一年，股票A的收益率、GDP的增长率和通货膨胀率之间的关系。通过线性回归，可以确定一个平面。
平面在GDP增长率方向的斜率为0.65，表示股票A的收益率对GDP增长率变化的敏感度为0.65。如果GDP增长率变化1％，则股票A的收益率变化为0.65×1％为0.65％。
平面在通货膨胀率方向的斜率为-3.5，表示股票A的收益率对通货膨胀率变化的敏感度为-3.5。
敏感度符号说明，当预期GDP增长率或者通货膨胀率增加时，股票A的收益率相应地增加或者减少。对于大部分公司来说，通货膨胀率上升是坏消息，因此通常通货膨胀率的敏感度是负数。
平面的截距表示A的零因子收益率为2.6％，也就是说两个宏观因素如果期望值取值为零的话，股票A仍具有的期望收益率为2.6％，这是不受时间和因素影响的其他因素对股票A的收益率带来的固定的影响。
A的实际收益率与平面上对应点的差为收益率的随机扰动项部分。例如，A在第六年由双因素模型生成的期望收益率为14.5％（在样本回归平面上的点），而第六年的实际收益是18.9％，那么随机项为4.4％，是由股票A公司层面上的个体非系统风险带来的随机收益。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
