市场模型的实际应用及方程解析

在因素模型的实际应用过程中，人们常用市场指数来作为影响证券价格的单因素，此时的单因素模型被称为市场模型。市场模型实际上是单因素模型的一个特例，比如可以用沪深300指数来作为单因素解释中国A股股票的收益率变化。

假设一种股票在某一特定时期内的收益率与同一时期市场指数（如沪深300指数、上证180指数、美国的S＆P 500、标准普尔500指数等）的收益率相联系，即如果行情上扬，则很可能该股票价格会上升，市场行情下降，则该股票很可能下跌。因此，可以用市场模型的方程表示这一关系：

式中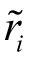：代表某一给定时期证券i的收益率；

I代表市场指数；

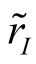代表相同时期市场指数I的收益率；

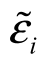是随机扰动项。

例子：

考虑股票A，其单因素模型中的ai=4％（不随时间变化的其他因素对股票A收益率的固定影响是2％），βi=1.5（股票A的收益率对市场指数收益率变化的敏感度是1.5，根据上一章所讲的根据贝塔值来分类股票，股票A的贝塔值大于1，说明是进取型的股票）。根据这些给定值，可以写出股票A的市场模型：

根据市场模型，如果市场指数收益率为10％，则证券A的收益率预期为19％（等于固定影响的4％，再加上随市场指数变化带来的收益率1.5乘以10％）。可见，由于A是进取型股票，在市场涨10％的情况下，股票A的收益率高于市场的收益率，能涨19％。

同样，如果市场期望收益率为-10％，由于股票A的进取性，它的期望收益率为-11％，也随着市场一起下跌。

这里需要注意的是，由于随机误差项的存在（表示证券收益率中没有被市场模型所完全解释的部分），当市场指数上升10％或下降10％时，证券A的收益率将不会准确地为19％或-11％。也就是说，实际收益率和指数模型算出的期望收益率之间的差将归结于随机误差项的影响，是由公司个体风险带来的随机收益。(www.xing528.com)

例子：

假定股票A与B的指数模型由下列式子估计：

已知市场组合的标准差　σM=　20％，股票A和股票B的随机扰动项的标准差为：σεA=　30％，σεB=　10％。求每个股票的方差和它们之间的协方差，若将股票A和股票B组成等权重的组合，那么组合的非系统风险是多少？

由基于单因素模型证券的方差可以写成系统风险和非系统风险相加，可求出：

A和B的协方差为：

这里就没有随机扰动项之间的协方差了。

由A和B组成等权重的组合：

组合p的方差：

组合p的方差也分成两个部分，是其中的系统风险部分，是非系统风险部分。由于随机扰动项之间是不相关的，所以非系统风险部分只包括两个股票的方差部分：