单因素模型在投资学中的定义和应用

单因素模型是描述证券收益率生成过程的一种模型，因素往往以指数形式出现，如股票市场指数、国民经济增长指数、通货膨胀指数等。

因素模型提供了关于证券收益率生成过程的一种新视点。可以用一元或者多元回归统计分析，以一个或者多个变量来解释资产的收益，从而比仅仅以市场来解释证券的收益更准确。

因此，单因素模型相对CAPM解决了两个问题，一是提供一种简化地应用CAPM的方式；二是细分影响总体市场环境变化的宏观因素，如国民收入、通胀率、利率、能源价格等具体带来风险的因素，以及影响大多数资产收益率的其他因素。

例子：以一元回归分析得出单指数或单因素模型

假设经济增长（GDP增长率）对股票收益率有普遍影响，且只考虑GDP变化对资产收益率的影响。

通过历史数据库，可以得到表5-1中的数据。这是10年GDP增长率和某证券收益率的数据，是时间序列的数据。我们可以把六年的两个变量的数据点在横轴是证券收益率，纵轴是GDP增长率的坐标系中。这样可以得到图中散落的十个点。

表5-1　某证券各年收益率和GDP增长率

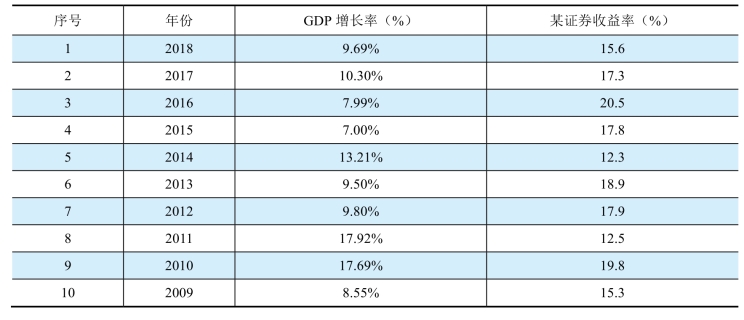
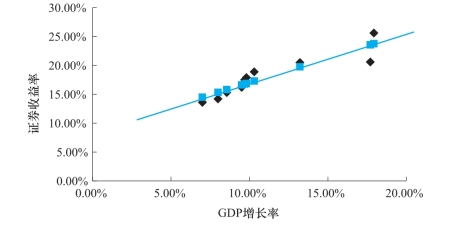
图5-1　某证券收益率和GDP增长率的线性拟合图

基于证券收益率和GDP历史的数据，可以利用一元回归的方法，回归出样本回归直线，即图5-1中的直线，其回归方程为r=0.085+0.85GDP。

给定任一证券的实际收益率，由于含有非因素收益率而位于拟合直线的上方或下方。对例子中的单因素模型反映的关系的完整描述为：

斜率0.85的含义是，当GDP变动1％的时候，证券的收益率变动是0.85。所以斜率表示证券的收益率对因素变动的敏感度，斜率越大，该资产的因素敏感度就越大。截距项0.085表示不随时间变化的其他因素对证券收益率的固定影响，包括无风险收益率对证券收益的影响。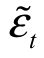为随机扰动项，表示在某个时间t时，证券收益率落在回归直线的上方或下方，离直线的距离。其含义是证券收益率中不随因素变化而变化，除固定影响之外的由公司特有风险带来的随机收益。

单因素模型的一般形式为：

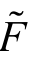一般地，单因素模型认为有一个因素对证券收益产生广泛影响，这里也是随机变量，它是宏观因素或其他有广泛影响的因素变化。

从方程中可以看出，任何一个证券的收益由三部分构成：

1.ai是宏观因素的期望为零时，该证券的期望收益； (www.xing528.com)

2.bi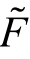是系统性风险收益，即随宏观因素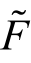变化而变化的不确定的收益，且资产收益率随因素变化的敏感度是bi，也常被称为因子载荷（Factor Loading），能够直接通过回归方法估计出来。由于敏感度体现的是证券或组合相对于因素变化而变化的程度，所以也是该证券或组合承担的系统风险的衡量，或者说是该证券或组合在风险因子上的暴露程度。例如，说某个资产在宏观经济波动上风险暴露程度很大，指的是这个资产的收益会因宏观经济波动而具有更大的波动性，来自宏观经济波动因子的系统风险较大；

3.是与GDP无关因素的作用，是非系统性风险带来的随机收益，即只与单个资产相关的非预期事件形成的非预期收益。它是均值为零的随机变量。

这里有两个重要的假设：

1.随机误差项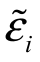与因素不相关，，意味着因素对随机误差没有任何影响。

2.任意两种资产的随机误差之间不相关， ，意味着一种资产的随机误差对任意其他资产的随机误差不产生任何影响。即，两种资产的收益率仅仅通过对因素的共同反应而相关联。

基于单因素模型的计算：资产i的期望收益、方差和两种资产之间协方差。

期望收益率：

2.任意两种资产的随机误差之间不相关，

单因素模型中，可以得出资产i的方差为：

方差也分成两部分：（1）和因素相关的部分；（2）非系统风险的随机扰动部分。

协方差：协方差中不包括随机扰动项之间以及随机扰动项和因素之间的协方差，是因为资产之间的随机扰动项的协方差为零，随机扰动项代表的收益变化和因素变化也不相关。

基于上式也可以这样来理解由因素模型生成的资产收益之间的协方差：

资产之间的相关性，或者说资产收益率的同向性，来自它们共同受到同一个因素的影响。因为它们的公司层面上的风险是独立的，不相互影响。所以资产之间的联系，就是受共同因素的影响。

因此，可以总结出因素模型的两个重要特征：

1.因素模型能够克服马科维茨模型的庞大计算量的困难。如果组合里有n项资产，计算组合的方差—协方差矩阵需要进行个方差和不同协方差的测算。但因素模型 中，由因素模型生成的两个资产的协方差等于，因此，只需要测算n个bi和1个σF就可以了，大大减少了计算量。

2.分散化。

根据资产i的方差　，资产的方差可以分成两部分：一部分是和因素敏感度相关的系统风险项，另一部分是后面的随机扰动项方差，即非系统风险部分。

由因素模型生成的资产收益的方差中，随机扰动项方差是非因素风险也是非系统风险，非系统风险会随着股票数目的增加而逐渐被分散掉。证明过程和上一章4.7中的n趋于无穷大时非系统风险被分散掉的证明是一样的。