投资学教材：总风险分解技巧

如果把CAPM中的期望收益的期望符号打开，那么单一证券的随机收益率满足：

因为打开了期望符号，所以在后面加上随机扰动项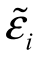，且，意味着随机扰动项的期望值为零，随机扰动项代表的随机收益与市场组合的随机收益之间不相关。

证券i的随机收益可以用上式表示，那么可以求出证券i的方差如下：

则投资组合i的风险（方差）可以由两部分组成：非系统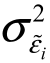风险　与系统风险。

性质1：高度多样化的组合，其非系统风险几乎被完全分散，其系统风险趋向两两协方差的平均值。

证明：

当组合p充分分散化，n　→∞时，不妨设，每个证券的权重均为，且为平均的方差，为平均的协方差。则组合p的非系统风险和系统风险分别为：

性质2：如果单一证券的非系统风险是有界的，即：

且不同证券之间的误差项不相关，即：

则在一个高度多样化的投资组合p中，投资组合的方差与　无关，即　在投资组合中被分散了。

证明：

单因素模型：

p为有n个i这样的资产形成的充分分散化的组合，(www.xing528.com)

由于公司层面的非系统风险带来的随机收益之间不相关，且随机扰动项收益与市场组合收益也不相关，所以：

是只和资产i有关的非系统风险，即投资者可以通过高度多样化的投资组合分散这部分风险。那么在均衡定价时，这部分风险是不会被市场所承认的，所以对单一证券定价时，只有系统风险才被市场所承认，获得相应的风险补偿。

说明：

1.高度多样化的投资组合与前沿边界上的投资组合的关系。

n种风险资产和一种无风险资产的线性前沿边界上的组合是没有非系统风险的，这是由有效前沿边界组合的性质决定的。因为线性前沿边界有效组合上的所有组合都在一条线上，所以是完全线性相关的。可以回忆3.8节“两种风险资产”的情形，两种风险资产相关系数为1时，可行集是两者的连线。

2.组合的贝塔值是组合中各个资产贝塔值的加权平均：。β值具有线性可加性。

证券市场线的含义：

1.市场组合将其承担风险的报酬按照每个证券对其系统风险承担的大小βiM（单位化的协方差）分配给各证券。

2.市场组合的风险溢价是证券市场线的斜率，可以看成单位市场风险的价格。

3.市场组合的总风险只与各项资产与市场组合的风险相关性有关，而并不依赖于各项资产的总风险（各项资产的方差）。

4.β值越大，则该项资产对市场组合的影响就越大，在市场均衡时，该项资产应该得到的风险补偿也就越多。