证券市场均衡条件与投资学书籍讨论

1.经济中投资者的总财富等于所有资产的总市值。

2.证券的价格使得对每种证券的需求额正好等于市场上提供的证券市值。

3.无风险利率使得对资金的总借贷量净值为0。

首先，假设市场上只有两类投资者，一类进行无风险借入，另一类进行无风险贷出。根据均衡条件3，无风险借入的资金正好等于无风险贷出的资金。借入者用从贷出者处借来的资金加上自己的初始财富，又都全部投资于风险资产了。相当于整体上投资者手中的财富全部投资于风险资产了。根据均衡条件1，投资者的总财富全部投资于所有风险资产，所以总财富等于风险资产总市值。

其次，根据分离定理，投资者如果持有风险资产，一定按照切点组合的权重来投资。那么投资者的总财富全部投资于风险资产，且对风险资产的配置权重就是切点组合的权重。如果把切点组合看成对风险资产的需求方面，把市场组合看成对风险资产的供给方面，根据均衡条件2，当市场均衡时，切点组合就是市场组合。

在市场均衡条件下，如果所有的风险资产都是严格正供给的，则市场组合的风险溢价一定是严格正的。

情况一

当全局最小方差点mvp的纵坐标A/C大于rf时，双曲线和斜率为正的那条射线相切，如图4-2所示。

投资者将在射线FT上进行投资，按照不同的比例投资于无风险资产F和切点组合T。可行集如图4-3所示。

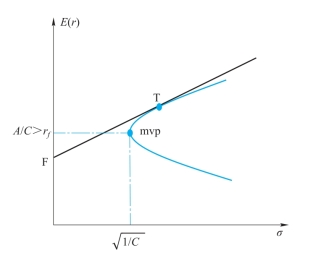
图4-2　A/C大于rf时的情况

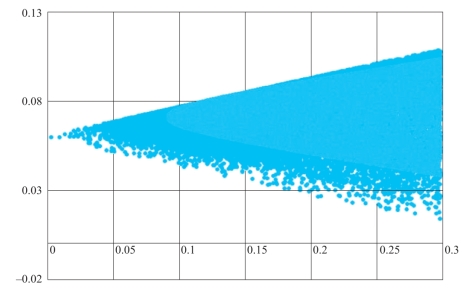
图4-3　A/C大于rf时的可行集（蒙特卡洛模拟）

情况二

当全局最小方差点mvp的纵坐标A/C等于rf时，两条射线的前沿边界就成了双曲线的两条渐近线，如图4-4所示。

由于双曲线和射线没有切点，所以投资者将在F点投资。因为无法满足均衡条件3，即无风险资产的借贷净值为零，因此市场均衡时情况二不会出现。(www.xing528.com)

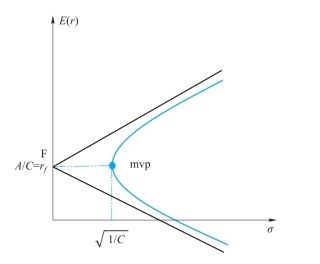
图4-4　A/C等于rf时的情况

这种情况下，投资者并不是不投资于风险资产，而是对风险资产的投资权重之和为零，对风险资产的投资是自融资的。图4-5是三种风险资产自融资的可行集，是顶点在期望收益轴的两条射线及其之间的区域。可以证明，n种风险资产自融资的可行集都是两条射线及其中间的区域。

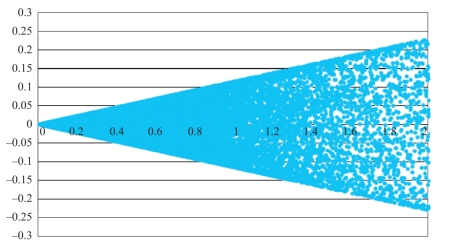
图4-5　三种风险资产自融资组合的可行集

当风险资产自融资组合加上一种无风险资产且A/C等于rf时，可行集的形状不变，但两条射线的顶点会变成rf，如图4-6所示。

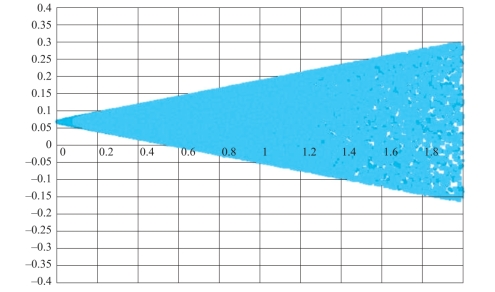
图4-6　三种风险资产加入无风险资产后，A/C等于rf时的可行集

情况三

当mvp的横坐标A/C大于小于rf时，双曲线和斜率为负的那条射线相切，切点是T'，如图4-7所示。

投资者将卖空风险组合T'，用卖空的资金加上原有资产投资于无风险资产F。无法满足均衡条件2和3，因此市场均衡时，情况三不会出现。

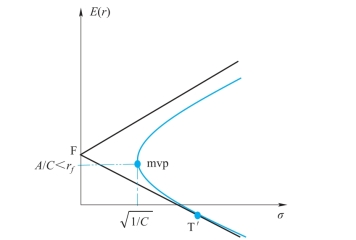
图4-7　A/C小于rf时的情况

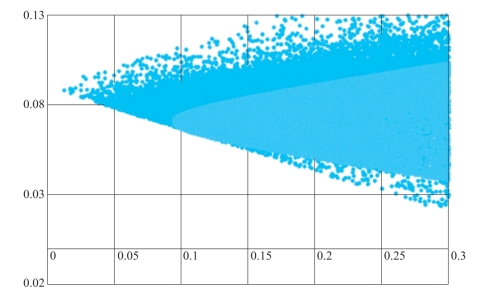
图4-8　A/C小于rf时的可行集（蒙特卡洛模拟）