【摘要】：因为无风险资产是没有风险的，它和任何风险资产的协方差等于零，所以无风险资产的加入不影响原有风险组合的方差。图3-31加入了无风险资产的前沿边界变成了两条射线后，根据有效集的定义，只有斜率为正的上面那一条射线才是有效集。图3-32加入无风险资产后的可行集
因为无风险资产是没有风险的，它和任何风险资产的协方差等于零，所以无风险资产的加入不影响原有风险组合的方差。
构造如下拉格朗日函数：
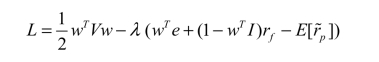
一阶条件为：
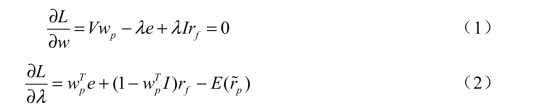
由（1）和（2）得到：
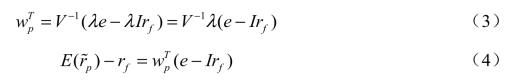
将（3）带入（4）得：
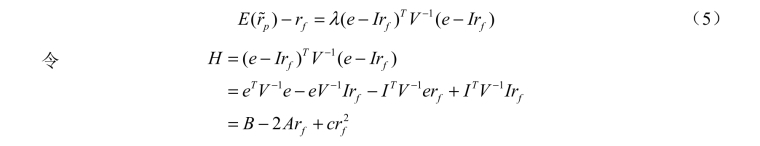
通过求H的判别式可知，无论rf的取值如何，H为大于零的数值。
由（5）得到：
将（6）带入（3），得到（7）式，明确地解出了最小方差组合的权重向量w*：
将（7）带入n种风险资产和1种无风险资产的组合方差中，
，得到：
(www.xing528.com)
可以得出，最小方差组合是两条截距相同、斜率相反的射线。
前沿边界由双曲线变成了两条从（0，rf）出发的射线，如图3-31所示。
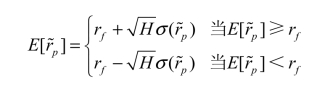
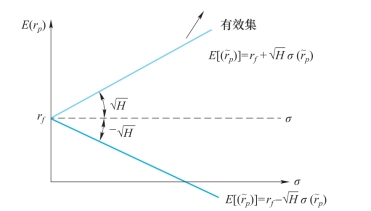
图3-31
加入了无风险资产的前沿边界变成了两条射线后，根据有效集的定义，只有斜率为正的上面那一条射线才是有效集。
任意组合q与前沿组合p之间的协方差为：
由于wp是前沿组合，所以可以用（7）式带入，得：
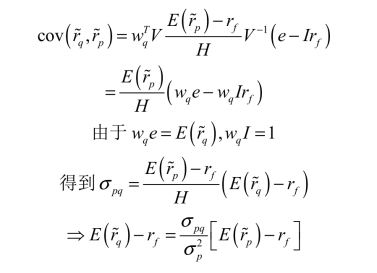
因此，任意组合q与前沿组合p的期望收益以及方差协方差满足如下式子：
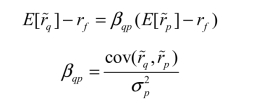
上面这个关于
的式子已经和下一章所要导出的资本资产定价模型非常相似了，但只是形似，如果要达到神似，需要加上下一章所要讨论的“市场均衡条件”。
图3-32为加入了无风险资产后的可行集，可以看出可行集的上下边界为两条射线，而上边界的射线为有效集。
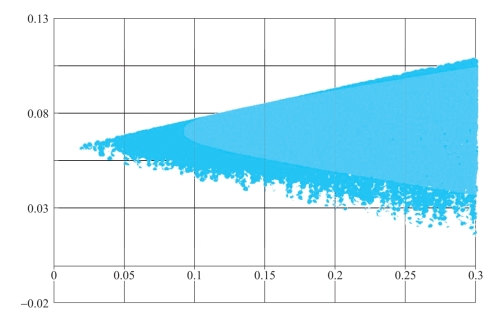
图3-32 加入无风险资产后的可行集（蒙特卡洛模拟）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
