【摘要】：在解的过程中需要设四个字母A，B，C和D，它们分别代表四个数，表示不同的向量矩阵相乘。任何有效前沿边界上的组合权重都可以表示成式的形式，而且任何权重可以表示成g+hE（)形式的投资组合都是前沿边界上的投资组合。再进一步看，任何两个前沿边界资产组合p和q的收益率协方差为：根据式子将p和q这两个前沿边界组合的wp和wq代入到wqVTwq中，得到：当q和p重合成一个组合p的时候，协方差就变成组合p的方差了。
需要解决的问题是约束条件下的最优化问题，可以采用拉格朗日乘子法（Lagrange Multipliers）来求解，设wp是这个式子无约束问题的解，可以构造拉格朗日函数：
其中λ，γ为两个正的常数，下面三个式子是一阶条件：
拉格朗日函数分别对w，λ和γ求导等于零。
由（3）式可得：
将（6）分别带入（4）和（5），得到（7）和（8）两个式子：
通过（7）和（8）可解出λ和γ。在解的过程中需要设四个字母A，B，C和D，它们分别代表四个数，表示不同的向量矩阵相乘。
A=ITV−1e=eTV−1I
B=eTV−1e
C=ITV−1I
D=BC−A2
因为方差—协方差矩阵V是对称正定矩阵，所以V − 1仍然是对称正定矩阵，所以B＞0且C＞0，也可以推出D＞0。(www.xing528.com)
可以解出：
将（9），（10）带入（6）可得：
其中g和h都是n维的列向量：
在V，e已知的前提下，A，B，C，D以及g和h都可以明确求解。
任何有效前沿边界上的组合权重都可以表示成式（11）的形式，而且任何权重可以表示成 g+ hE（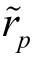
)形式的投资组合都是前沿边界上的投资组合。再进一步看，任何两个前沿边界资产组合p和q的收益率协方差为：
根据式子（11）将p和q这两个前沿边界组合的wp和wq代入到wqVTwq中，得到：
当q和p重合成一个组合p的时候，协方差就变成组合p的方差了。
令q和p相同，通过简化，（12）式可以变形为：
（12）式是关于前沿边界上组合p的期望收益和标准差的式子，可以看出来，这个式子其实就是双曲线的表达式。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
