投资学：风险资产前沿边界推导

本节通过数学推导和数据模拟，进一步讲解n种风险资产的有效集和可行集。

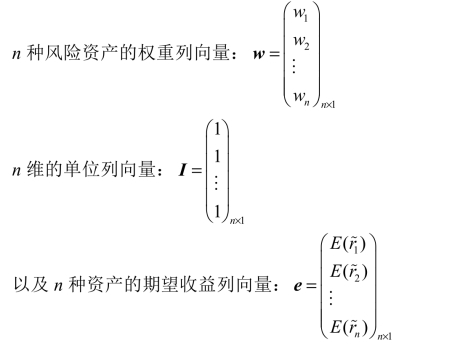
假定n维向量w表示投资于n种风险资产的权重，该向量满足　w≠0，各个风险资产的供给为正。

又假设方差协方差矩阵V是正定对称矩阵，从而wTVw＞0，前面的内容介绍过，wTVw是n种风险资产组合的方差，说明风险资产组合的方差是严格大于零的。可以把风险和期望收益权衡的问题，看成是解一个二次规划的问题。

定义几个向量：

风险—收益权衡问题（二次规划问题）可以表示为：

(www.xing528.com)

为什么是二次规划问题？

目标函数中组合的方差乘以，是为了后面利用拉格朗日乘子法求极值时的数学证明方便。n种风险资产组合方差的向量矩阵相乘的形式，可转化为n2项方差和协方差相加的形式：

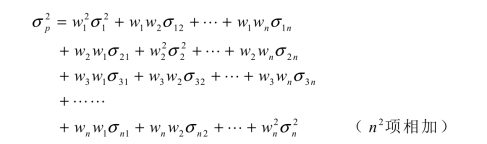
这里的未知数是n种风险资产的权重w，每一项都是关于未知数w的二次项，所以这是一个二次型。二次型作为目标函数，在数学上是一个二次规划问题。

这个二次规划问题要求解的未知变量是n种风险资产的权重。根据第一个约束条件，在组合的期望收益率达到某一个水平时，可以求出的一组最优权重w，就是在期望收益下，能达到的最小方差组合。

如果不断的变化第一个约束条件中的期望收益水平，能解出每个期望收益水平下的最小方差组合，将会得到一系列的最小方差组合的权重向量w*，这些向量对应组合的均值和标准差就形成了一条双曲线。由于双曲线上的组合都是一定期望收益下的最小方差组合，所以也称之为最小方差前沿边界。

图3-25　n种风险资产双曲线最小方差前沿边界