3种风险资产和1种无风险资产在《投资学》中的应用

本节讨论更为复杂的情况：两种风险资产和一种无风险资产构成的组合。

例子：

已知无风险资产的收益率为4％，股票A的期望收益率为10％，标准差为15％，股票B的期望收益率为15％，标准差为20％。相关系数为0.5，求三种资产组成的新组合中最小方差组合权重为多少？三种资产形成组合的最大夏普比率是多少？如果投资者的效用函数为：，求投资者的最优风险配置组合中各资产所占的比重。

求解这种情况下的最优风险资产，需要分成两个步骤：

第一步，找出两种风险资产和一种无风险资产情况下方差最小的可行集合（切线）。

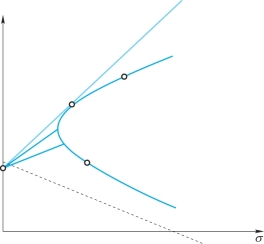
图3-12　两种风险资产和一种无风险资产的最小方差可行集合

第二步，结合无差异曲线，找到最优风险组合（切点）。

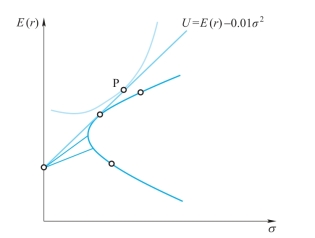
图3-13　两种风险资产和一种无风险资产的最优风险配置组合

第一步：求出2个风险资产和1个无风险资产的方差最小集合。如果两个风险资产形成的可行集合是双曲线，由3.4节介绍的一种风险资产和一种无风险资产的情形可知，这条双曲线上的组合与无风险资产F有无数条连线，可以想象，这三种资产形成组合的可行集不再是某条线，而是两条射线之间的所有区域（证明在后面的3.15节）。可以发现，同一个期望收益水平上，方差最小的组合都在上面的那条射线上。可想象在每个期望效用水平上画出水平线，同样的水平线上，最左边的方差最小的点就形成了上面的射线。为了求出这条射线，需要设置的目标函数是，组合的夏普比率最大，约束条件是，这个组合在这条双曲线上。即，在双曲线上找到和无风险资产连线斜率最大的那个点，也是双曲线和最小方差切线的切点T。

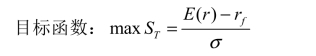
约束条件：E（r）=wAE（rA)＋wBE（rB)

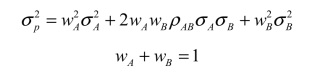
求出最大斜率资本配置线和双曲线T中，A资产的权重：(www.xing528.com)

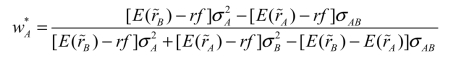
这里求出的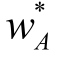是切点组合T中股票A所占的比例。

第二步：找出最优风险组合。设最优风险组合中，T点的权重为yT，最优风险组合由F点和切点T组成。

目标函数：maxU=E（r)−0.05Aσ2

约束条件：E（r)=(1-yT）×rf+yT×E（rT)

将约束条件代入目标函数，得到效用u关于yT的二次函数：

再对目标函数求极值，得到效用最大时在资产T上的最优投资比率：

这里求出的是最优风险配置组合中切点组合T所占的权重，

是最优风险配置组合中无风险资产权重。而在最优风险配置组合中股票A和股票B占的比重分别为：

从图3-13看，最优风险组合就是最小方差切线和投资者无差异曲线的切点P。

那么n种风险资产和一种无风险资产的情形如何呢？和上面这种情况是非常相似的（证明在3.15节），n种风险资产形成的可行集的最小方差组合集合仍然是双曲线，其他组合都在双曲线的右边区域。明智的投资者都会选择在最小方差组合的集合——双曲线上投资。再加上无风险证券的投资，就和两种风险资产和一种风险资产的情形一样了。

对于上面的例题，可以求出：