投资学：无差异曲线在期望收益—标准差平面上的应用

无差异曲线是经济学中进行效用分析的基本工具。在某个投资者无差异曲线上，其效用水平是相同的。那么在期望收益—标准差平面上，投资者的无差异曲线是什么样的呢？

首先，第二章介绍了一个比较常见的投资者效用函数：

这个效用函数中只有期望收益和标准差，投资者的效用水平随着金融资产期望收益的增加而增加，随着金融资产收益波动的方差（风险）的增加而减少，说明拥有这种效用函数的投资者是风险厌恶的。式子中的A表示风险厌恶程度，A越大表示同样风险的增加能带来该投资者更大程度的效用减少。需要说明的是，效用函数中的期望收益和标准差需要带入百分号前的数值。

假设投资者的效用水平在不变，可以用标准差来表示期望收益，得到：

上式表明，期望收益是关于标准差的二次函数，是一条开口向上的抛物线。

且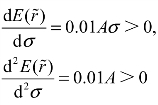 ，说明风险厌恶投资者（A＞0）其无差异曲线是向右上方倾斜的，且是向上弯曲的，弯曲程度越大，其风险厌恶程度越高。或者反过来，其风险厌恶程度越高，无差异曲线的弯曲程度更大。(www.xing528.com)

从微观经济学中对无差异曲线的定义来看，同一个投资者的无差异曲线会密密麻麻地分布在整个平面中，且不会相交。对于风险厌恶投资者的无差异曲线，越往坐标系的左上方，效用水平越高。因为，根据效用函数　可知，效用是随着期望收益的增加而增加的，同时效用也是随着标准差的变小而增加的，所以在期望收益—标准差的左上方，正是期望收益更大且标准差更小的区域。

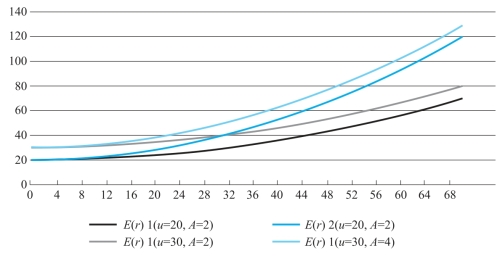
图3-6　无差异曲线

从图中可以看出，更加弯曲的深蓝和浅蓝色的两条线是风险厌恶程度A更高的投资者，因为当标准差（风险）等量增加时，这个投资者需要更多的期望收益的增加来补偿风险的增加。

而比较两条蓝色的无差异曲线，位置越靠左上方的曲线，投资者的效用越高，这是因为当承担的风险相同的时候，浅色的线总比深色的线上的期望收益高。因此，浅色的效用水平更高一些。

同样的道理，灰色和黑色的投资者风险厌恶程度更低一些，因为这两条线更平坦一些。而其中灰色的效用水平更高一些，因为灰色的无差异曲线在黑色的左上方。

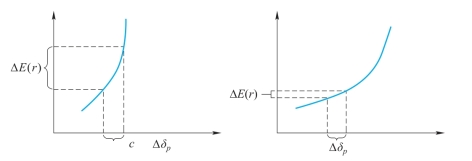
图3-7　不同风险厌恶程度的投资者的无差异曲线

可以比较一下图3-7中两个投资者的风险厌恶程度，很显然，左边的投资者的无差异曲线更加弯曲，所以这个投资者的风险厌恶程度更高。