资本配置线及其风险溢价-《投资学》摘要

这一节开始，将要在期望收益和标准差平面刻画资产组合的收益和风险特征。

按照从简单到复杂，分别讨论以下三种组合情况：

1.组合由一种风险资产和一种无风险资产构成

2.组合由两种风险资产构成

3.组合由两种风险资产和一种无风险资产构成

期望收益—标准差坐标系：

上面的期望收益—标准差平面（E-σ平面）中，横坐标为资产或组合的标准差，代表其风险；纵坐标为期望收益率，代表收益。这样的坐标系体现了金融资产的两个最关键的特性——风险和收益。这一章均值—方差分析法将全部在这一坐标系内进行分析。

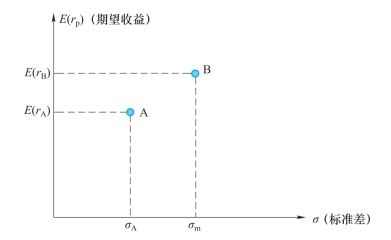
图3-1　期望收益—标准差坐标系

第一种情况：由一个风险资产与一个无风险资产构成组合

随着两种资产的投资比率（权重）不同，组合在坐标系中的位置有什么规律呢？也就是如果有100万元用于投资在风险资产P和无风险资产F，那么随着这100万元在P资产和F资产上分配的比例不同，新的组合C将落在E-σ平面的哪里呢？

例如，已知风险资产P的期望收益率是15％，标准差是22％，无风险资产的收益率是7％，可以把这两种资产在期望收益—标准差平面画出来：

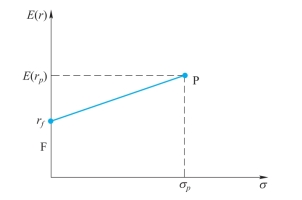
图3-2　一种风险资产和一种无风险资产

无风险资产对应着图中的F点，无风险收益率rf=7％，风险资产对应着图中的P点，期望收益率为15％，标准差为22％。(www.xing528.com)

作为风险资产，P点在F点的右上方，具有更高的风险，同时也有具有更高的收益率。

假设由风险资产P和无风险资产F组成的组合为C，那么组合的期望收益率E（rc）=wp×E（rp)+wf×rf，由数学准备7得到组合的标准差σc=wpσp，整理一下得到σc=wpσp，即　wp=σc/σp，将　wp带入E(rc)中，得到：

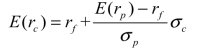
我们发现这个式子是一个关于组合C的期望收益率E(rc)和它的风险σc的直线方程。直线的截距是无风险收益率rf，斜率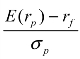是风险资产的风险溢价（E（rp)−rf）除以风险资产的标准差。可以看出，新的组合C在平面中的轨迹是一条经过无风险资产F和风险资产P的直线。

我们把这条线的斜率定义为酬报与波动比，也是夏普比率，它是资产的风险溢价除以标准差，是承担单位风险所要求的风险溢价（E（rp)−rf）。这条直线称为资本配置线（Capital Allocation Line，简称CAL）。

上面例子中的夏普比率为：（0.15-0.07）/0.22=0.36

并且直线FP上所有组合的斜率相同，直线上的所有组合的夏普比率均为0.36。

图形分析：如果全部资产都投资于风险资产P，则新的组合在P点，如果全都投资于无风险资产F，则新的组合在F点，随着两种资产的比例不断变化，新的组合就形成了资本配置线。组合C是在FP的连线上，随着对风险资产的投资比例增加，C从F点沿着直线FP运动到P点。

结论：由无风险资产和风险资产构成的任何一种组合都将落在连接它们的直线上；其在直线上的确切位置将取决于投资于这两种资产的相对比例。该直线称为资本配置线（Capital Allocation Line），斜率（酬报与波动比，夏普比率）表示每增加一单位标准差上升的风险溢价，或者表示单位额外风险的额外收益。

专栏：夏普比率（Sharpe Ratio）

夏普比率由诺贝尔经济学奖获得者威廉·夏普提出，用于帮助投资者了解投资的回报与其承担风险的对比关系。这个比率表示的是，承担单位风险或总风险（组合的标准差来表示）所获得的超过无风险收益率的回报（收益）。

一般来说，夏普比率越大，风险调整后的回报就越有吸引力。

夏普比率可用于评估投资组合（比如共同基金（Mutual Fund）过去的业绩表现），其中实际回报用于公式。

夏普比率还有助于分析投资组合的收益是由明智的投资决策还是风险过大带来的。虽然一个投资组合或基金可以享受比同行更高的回报，但只有那些更高的回报不带来额外的风险，它才是一个很好的投资。

目前可以很容易地从财经类基金网站上得到各个基金的净值增长率的排名。但是如果我们理解了夏普比率就不会直接按照净值增长率来买排名靠前的基金，而是进一步计算出各只基金的夏普比率，选择夏普比率更大的基金来考虑投资。