投资学：绝对和相对风险厌恶系数结论

对上图的观察使我们可能产生一种直觉，即如果效用函数越是凹向横轴，也就是弯曲程度越大，投资者的风险厌恶程度就越大。

假设随机收益是在初始财富附近变化的一个微小的量，其均值为零，方差为σ平方，，并满足公平赌博的定义：

将确定性等值的式子两边，在初始财富附近做二阶泰勒级数展开：

其中Re为高阶余项，通过化简整理得：

其中σ为x的标准差，可以将如下式子作为风险厌恶度量的测量指标，而且它不受量纲影响。

于是阿罗-普拉特绝对风险厌恶系数（Arrow-Pratt Measures of Absolute Risk-Aversion）定义为：

可以看出这是一个没有量纲的表示效用函数弯曲程度的指标。由于二分之一和微小随机变化的方差都是和效用函数无关的，所以只取出其中负二阶导数除以一阶导数的值作为衡量投资者风险厌恶程度的指标，并把这个指标称为阿罗-普拉特绝对风险厌恶系数。对于风险厌恶的投资者来说，效用函数的二阶导数是小于零的，所以这个指标是大于零的，值越大，说明投资者风险厌恶程度就越高。

关于这个指标，需要说明的是：

第一，绝对风险厌恶系数是一个局部概念，依赖于初始财富水平，因此只适用于初始财富附近微小的随机变化量。

第二，这个系数依赖于效用函数的形式，如果初始财富一样，效用函数不一样，则有不同的风险厌恶程度。面临相同的公平赌局，会要求不同的风险补偿，因此可以衡量不同的决策者在特定的财富水平下的风险厌恶程度。

第三，这个系数对效用函数的正仿射变换具有不变性。因为正仿射变换并没有改变所描述的偏好顺序，具有一致性。

提问：绝对风险厌恶系数和马科维茨风险溢价的区别是什么？

求出的阿罗-普拉特绝对风险厌恶系数是一个关于初始财富w0的函数，可以把这个函数继续对初始财富进行求导。(www.xing528.com)

如果这个导数小于零，∀w，有，说明随着投资者财富水平的提高，投资者的风险厌恶程度是递减的，这与现实情况是比较相符的。当人们变得越来越富有的时候，他们的风险厌恶程度是降低的。

如果这个导数大于零，∀w，有，则正好相反，当人们变得越来越富有的时候，他们的风险厌恶程度是增加的。这似乎和我们的日常生活经验有些不同。

如果这个导数等于零，∀w，有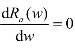，说明这是一个风险厌恶程度不随财富水平变化的投资者。

相对于财富而言，其中递减绝对风险厌恶意味着风险投资是一种正常品，随着财富的增长对风险投资的需求也是递增的，而递增绝对风险厌恶隐含着风险投资是一种劣等商品（Inferior Goods）。

如果将绝对风险厌恶系数乘以财富水平，就是一个受初始财富水平影响的相对风险厌恶系数（Measure of Relative Risk-Aversion）。

如果将绝对风险厌恶系数倒过来，就是风险承受指标，可见当投资者风险厌恶程度越高时，他的风险承受能力是越差的，所以两者成倒数关系。

有几种常见的风险厌恶特征的效用函数形式，属于双曲绝对风险厌恶或者线性风险承受函数，它们通常采取这种形式：

随着其中参数的设定不同，它们会变化成不同形式的效用函数。

不妨求出它们的各种风险厌恶程度衡量指标，就知道为什么这类函数叫双曲绝对风险厌恶函数，或者是线性风险承受函数。

下面是金融研究者广泛使用的一个函数，资产组合的期望收益为E(r)，其收益方差为σ2，其效用值为：

u=E(r)-0.005Aσ2

其中A为投资者的风险厌恶系数。方差减少效用的程度取决于A，投资者越厌恶风险，对风险投资的回避程度越大。