确定性等值与风险溢价：投资学视角

一个风险厌恶的投资者是不会参加一场期望收益等于入门费的公平赌博的，但赌场老板将入门费设置得足够低，总能吸引投资者参加赌博。

例如，一个期望收益为15元的赌局，如果入门费由15元降为12元，就会有人愿意参加这场赌局。这入门费由15元降到12元的差值3元，就可以看成是“引诱”风险厌恶者参与赌博的“风险溢价”，或者说是对投资者因参加公平赌博而承担风险的风险补偿。而这个事先确定付出12元的效用，和投资者参加一个期望收益为15元的赌博带来的期望效用是相等的。所以，12元就是这个赌博的确定性等值。

确定性等值是一个确定性的收入，这个收入给投资者带来的效用，和一个赌局给投资者带来的期望效用是一样的。

上面的例子中，12元是确定性等值，3元是马科维茨风险溢价，是为了吸引投资者参加赌博而降低的入门费，可以看成对投资者参加赌博并承担风险的补偿，所以称之为“马科维茨风险溢价”（这里的“风险溢价”为“马科维茨风险溢价”，下一章中“风险溢价”指的是资产的收益减去无风险利率的部分）。

确定性等值的计算公式为：

式子的左边是参加赌博的期望效用，等于右边一个确定性财富带来的效用水平，这个确定性的财富水平就是确定性等值（Certainty Equivalence）。

不同角度理解：

1.对投资者来讲，公平赌博虽然期望收益为0，但是投资者是不愿意接受的，觉得有风险的零相当于一个负的确定性的收益，所以他宁愿放弃一定的确定性财富来避免一个有风险的公平赌博。(www.xing528.com)

2.对于赌场老板来说，一个正期望收益的公平赌博，需要投资者交一个正的入门费。但是投资者是风险厌恶的，觉得这个正的期望收益不值一个等额事先确定交出的正的入门费，只值一个较少的确定性的付出。所以这个较少的确定性的付出就是和有风险的期望效用水平一样等值，而降低的入门费是赌场老板为了让风险厌恶投资者参加赌博的风险补偿，是风险溢价。

通过图2-3可以看出，A点是参加赌博的期望收益水平，A点高度对应效用函数上的B点，而B点所对应的财富水平CE就是确定性等值。

赌博的期望收益w0和确定性等值的差值π，就是投资者为了避免一个公平赌博而愿意放弃的一部分财富，我们称之为“马科维茨风险溢价”。

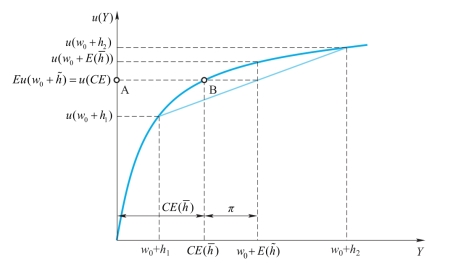
图2-3　效用函数和确定性等值

可以得到这样的结论：马科维茨风险溢价越大，确定性等值越小，投资者的风险厌恶程度就越大。

比如上面的例子中，入门费降低到12元时，如果投资者还是不愿意参加赌博，直到降低到10元才愿意参加，那么这个投资者就有更高水平的风险厌恶程度，他的确定性等值更低，需要的风险补偿更高（15元-10元=5元）。

这里需要说明的是，马科维茨风险溢价和确定性等值这两个指标是全局的指标（给出了某个效用函数的形式，就能求出确定性等值和马科维茨风险溢价，而不论具体的财富水平如何），代表具有某种形状的效用函数的投资者整体的风险厌恶程度，它们是有单位的。

下面再介绍一个不受量纲影响的衡量投资者风险厌恶程度的局部指标。