投资学-期望效用理论理论结果

这一节将介绍人们面对不确定性情况下的决策原则，即期望效用理论。

期望效用函数是消费者或投资者的一种投资决策准则。首先需要了解有哪些常见的投资决策准则。

收益最大准则：收益最大准则广泛应用于确定性的情况，按照这一法则，只需选取收益率最高的投资机会即可。经济学中的生产者理论和价值理论广泛使用这一准则。

在不确定性情况下，投资者的决策准则有：

第一，数学期望最大化原则（期望收益最大化），就是求出未来各种状态下的加权平均收益，权重是各个状态发生的概率。

第二，期望效用最大原则，求出未来各种状态下的加权平均效用，权重是各个状态发生的概率。本节将介绍期望效用理论。

第三，基于前景理论的价值最大化原则，这是在修正的效用函数——前景理论中的S型价值函数，以及在主观概率的基础上，根据计算出的加权平均价值来进行决策的准则。在行为经济学和行为金融学的课程中会有详细的介绍。

来看这样一个例子：

表2-2　几种投资方案收益

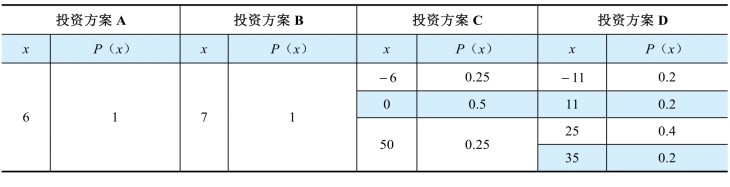
有ABCD四种投资方案，显然A和B具有确定性，概率p均为1，所以只用比较他们的收益谁更大一些。

对于C和D，是不确定性情况下的选择。可以用求均值的方法，求出C和D的均值分别为11和17，按照数学期望最大化原则，我们会选择方案D。

在还没有出现效用函数和期望效用之前，人们面对不确定情况时，直觉上大都是根据期望收益最大准则来做决策的。但这就是现实中人们面对不确定性时做决策的原则吗？先来了解一下著名的圣彼得堡悖论（The St.Petersburg Paradox）。

在18世纪，有这样一场掷硬币的赌博：如果硬币的正面朝上则赢得赌局。具体规定是：第一次翻到正面赢得2元，第一次输第二次赢得4元，前两次输第三次赢得8元……以此类推。一般情形为前n-1次输，第n次赢得2的n次方元。(www.xing528.com)

很显然，这是一个在任何情况下的期望收益都为正的赌博，作为赌场老板，是需要要求参与人先缴纳参加赌博的入门费才能参加这个赌博的。当时的人们都愿意支付多少入门费呢？

下面我们来看一看这个神奇的赌局。

表2-3　圣彼得堡悖论的收益

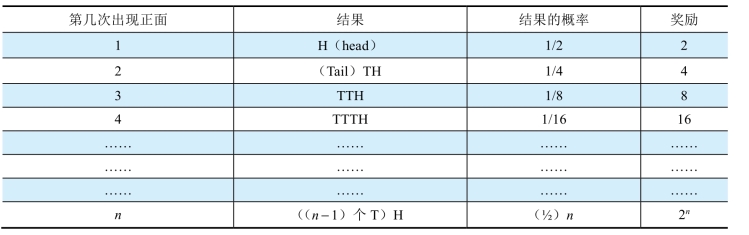
表2-3是这个赌局各个状态下的收益情况，先算一算这个赌博的期望收益是多少。

第一列和第二列表示这个赌局的n种状态，就是第几次出现正面；第三列是各个状态或者说各种结果的概率；第四列是每个状态下的奖励，也就是收益。

既然这个赌博的期望收益是大于零的，所以赌场老板不会免费让人来参加这个赌博，需要参与人事先支付一定金额的入场费。

下面的式子算出了这个赌博在n种状态下的加权平均收益，权重就是各个状态发生的概率。当n趋于无穷大的时候，这个赌博的平均收益也趋于无穷大。

通过上面对赌博期望收益的计算，入门费似乎也应该趋于无穷大。也就是说参与者无论交多少钱，赌博都会给他一个正的期望收益，花无穷多的钱都应该来参加赌博！

但在当时人们平均愿意支付的入门费却只有1～2元钱！为什么一场理论上无论花多少钱都有利可图的赌博，实际上人们只愿出如此低的入门费呢？

可见，期望收益最大原则并不能解决所有的不确定性问题，这一矛盾就是圣彼得堡悖论。

这个悖论的提出是对期望收益最大准则的质疑，是由瑞士数学家尼古拉斯·贝努利（Nicolaus Bernoulli）于1713年提出的。最终这个问题由尼古拉斯·贝努利的堂弟、当时圣彼得堡科学院院士丹尼尔·贝努利解决，其发表的论文刊登于18世纪的期刊——彼得堡科学院期刊（Papers of the Imperial Academy of Sciences in Petersburg，“Exposition of a New Theory on the Measurement of Risk”，1738）。这个问题后来也以“圣彼得堡悖论”而著称。

丹尼尔·贝努利的论文提出了解决“圣彼得堡悖论”的“风险度量新理论”，指出人们并不是用期望收益——“钱的数学期望”作为决策函数，而是用期望效用——“钱的函数的数学期望”来做决策的。