偏好与效用函数对商品排序

在确定性环境中，人们在做选择的时候，是建立在对不同选择的偏好关系上的，而偏好（Preference）是建立在消费者可以观察到的选择行为之上的。比如，相对于苹果来说，现在你更偏好吃一块巧克力。说明在苹果和巧克力之间，你更偏好巧克力。或者说，如果让你在心里对苹果和巧克力排序的话，你会把苹果排在巧克力的前面。可见偏好关系是对各种选择的一种排序。

但当人们真正做决策的时候，如果只有两三个选择还好，如果有成百上千个选择，显然对每个选择进行偏好排序就非常不方便了。但如果存在一种函数把商品（选择）集合通过某种规则映射到实数集就十分方便了，我们可以把商品（选择）间的偏好排序关系转化成实数之间的比较大小关系，这实在是太方便了！那么，这种映射或者说这种函数存在吗？这种函数的形式有什么特点，才能把人们对于商品（选择）的偏好关系转化成实数比较大小的关系？

可能大家已经想到，这个函数就是经济学中提到的效用函数（Utility Function），用效用来表示人们对不同商品的偏好。当函数值较大，说明这种商品或选择给我们带来的效用更高，我们越偏好这种商品或选择。效用函数将商品集合中商品之间的“偏好关系”（≽）转化成实数比较大小关系（≥），那么商品集合的各个商品之间的偏好排序或者偏好关系有什么特点呢？这就是一种二元关系。

商品集中的偏好关系可以用一种二元关系表述出来。

令C为商品集合或者消费集合，C中有M种可供选择的商品。它是M维实数空间RM中的一个非负的子集，且为闭集和凸集。x、y、z……是它的子集，称之为商品束或者消费束。每一个消费束可以看成一个M维的向量，向量中的M个元素分别代表对M种商品的消费。可以在消费束的集合上建立偏好关系。

这里需要说明的是，偏好关系是一种二元关系。

二元关系用通俗的话来解释，就是集合中任意两个元素，都可以进行比较。

二元关系：设S是一个非空集合，R是关于S的元素的一个条件。如果对S中任意一个有序元素对（a，b），我们总能确定a与b是否满足条件R，就称R是S的一个关系（Relation）。如果a与b满足条件R，则称a与b有关系R，记做aRb；否则称a与b无关系R。关系R称为二元关系。

偏好关系就是这样的二元关系，对于商品集合中的任意两个商品束，都满足偏好关系。对于偏好关系，我们可以做下面的定义：

（1）如果消费者在商品束x、y中“弱偏好”于x，即消费者认为x至少与y一样好，那么可以用这个式子来表达：x≽y；

（2）如果消费者“严格偏好”于x，也就是说在任何情况下，消费者都认为x比y好，则可以用式子x≻y来表达；

（3）如果消费者对商品x、y“无差异”，也就是说消费者认为两样东西同样好，则可以用这个式子来表达：x∼y。

也就是说偏好关系“≽”是用来描述投资者或者消费者对处于各种约束状态下的商品、服务和货币等资产进行比较的能力。

在经济分析中，为了确保消费者偏好表达的逻辑一致性，通常要求消费者的这种偏好顺序满足几个基本的公理。

假设理性的消费者有能力建立不产生矛盾的、一致性的偏好衡量标准或者排序准则，那么这样的假设就是消费者或者投资者的理性假设，他们都是理性人。这些公理包括：

完备性：对于两个消费束，总是存在着可比较的关系。

自返性：一个消费束，至少和它自己一样好。

传递性：如果认为x优于y，y优于z，那么x一定优于z。

具体而言，

完备性：每个投资者都具有一个偏好关系，且是完备的。这个投资者能确定x是否优于y，y是否优于x，或者两者同时成立，即他认为x和y是无差异的。对于任意两个消费束x和y，要么x≽y或y≽x，要么x∼y（两者同时成立），没有除此之外的任何情况出现，上面的几种情况已经是最完备的情形。

对于传递性需要注意的是，这个公理意味着这两种关系能被传递，体现理性人的逻辑自洽性，前后选择保持连贯性。传递性可以保证在一系列的两两之间的选择中，不会出现矛盾的循环，保持了偏好的一致性和逻辑性。

比如，苹果和香蕉之间你更偏好苹果；香蕉和梨子之间你更偏好香蕉；那么在苹果和梨子之间，你只能更偏好苹果，你才是一个理性的人。看起来好像是理所当然的偏好传递，和现实中人们的选择相比，其实这已经是一个非常强的理性假设了。现实中确实有很多人如果在苹果和梨子之间选择，偏偏更喜欢梨子，但这并不妨碍经济学家们把此当作一个重要的理性公理。(www.xing528.com)

如果偏好关系满足上述三种性质，即是理性的，它们也被称之为理性人的假设。

除此之外，为了能让偏好关系转化成比较实数大小关系的效用函数存在，还需要偏好关系满足连续性公理，其实质是指偏好关系不会发生突然的逆转。

连续性公理：如果消费集合C（C中有M种可供选择的商品，因此每个消费束C都是M维向量）中有若干的消费束Ci，i=1，2，……，所有Ci都不比消费集合中的某个消费束C差，即Ci≽C，i=1，2，……；而Ci，i=1，2，……收敛于（无限逼近于）一个消费束，则一定有≽C。

满足了上面的这些公理，就能证明效用函数的存在性。

定义：效用函数是一个实数u（·），对于偏好关系≽来说，消费集合中的两个消费束C和C’，如果C≽C’，则一定有u（C）≥u（C’），反之亦然。

定理（Debreu）：如果≽是消费集上的一个偏好关系，满足理性公理，就存在一个连续实数u（·），使得：

C≻C’⇔u（C）＞u（C’）

可见，一个效用函数可以为一个数值，数值的大小同消费者的偏好顺序一致。

用比较通俗易懂的语言来说，函数本质上是一个映射，是从一个集合到另一个集合的映射。而效用函数是从M维空间的商品集合映射到实数集合的一个映射。通过效用函数，把商品集的偏好关系转换成了实数集的实数大小关系。

有了效用函数的这种映射变换，对商品的比较变成了实数大小的比较，在数学分析上将更为便利。效用函数值越大的，人们对某商品就越偏好。

效用函数可以为每个商品束指定一个实数，数值上较大的表示它更为消费者所偏好。

这样获得的效用函数只是用来排列偏好的次序的，因此效用函数的特点是序数性。我们通常称之为序数效用函数。

序数性意味着：任意两个消费束之间的效用数值上的绝对差额是无关紧要的，那么就可能存在许多用来描述同一偏好顺序的函数，但三种效用函数反映了同样的偏好顺序。

如表2-1所示，这三种效用函数的具体形式虽然不同，但是对三种商品的效用值的排序都是一样的。具体效用函数值改变了，但是函数值之间的排序是不变的。

表2-1

这个结论可以一般化为以下定理：

一个效用函数通过正单调变换（Positive Monotonic Transform）而获得的另一效用函数与原来的函数表达同样的偏好顺序。

也就是说如果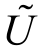（x　）≡f[U（x)]，且f(·)是单调递增函数，则有：

关于效用函数存在性的证明可以在中级或高级微观经济学的教材中找到，有兴趣的同学可以进一步学习和理解。

有了效用函数，在进行消费者决策行为分析的时候，我们就可以直接对效用函数求极值，得到消费者的最优选择。