基于信息交易量的股市投资者异质信念研究

在本书的4.1 节中基于Andersen（1996）的思想，我们对交易量进行了区分，将交易量区分为流动性交易量和信息交易量，并且认为由于投资者信念差异产生的交易量应该不包括流动性原因产生的交易量，因此基于信息交易量构造了异质信念代理变量。本节将对流动性交易量和信息交易量进行实证检验，并与本章第一节中总体交易量检验结果进行对比分析，检验在投资者异质信念的假设前提下，总体交易量、流动性交易量、信息交易量中的哪个变量作为信息流的替代变量更为合理？

首先，将流动性交易量LVt、信息交易量IVt分别加入到GARCH模型的条件方差方程中，对价格波动持续性参数的变化情况进行观察，模型定义如下：

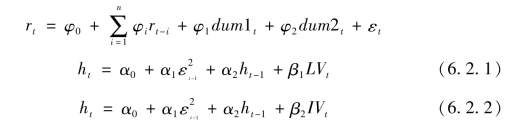
其中，dum1t与dum2t为虚拟变量，其定义与本章第一节中虚拟变量的定义相同。

美洲股票市场上，表6.8 的检验结果表明，对于道琼斯指数，对代表价格持续性波动的参数（α1+α2）的变化情况进行对比分析后发现，加入流动性交易量后持续性参数（α1+α2）为0.991，与本章第一节中未加入交易量时（α1+α2）为0.992 时的情况基本相同，仍然维持在接近于1 的水平。加入信息交易量后，持续性参数变为0.827，与本章第一节中加入总体交易量时持续性参数（α1+α2）为0.874 的情况相比，略有降低，说明信息交易量也能够在一定程度上吸收股票收益波动的持续性。此外，检验结果中流动性交易量的系数估计值显著为负，说明流动性交易量的增大能够降低市场上的收益波动。而信息交易量系数估计值显著为正，信息交易量的增加能够加速市场上的收益波动性。

表6.8 道琼斯指数信息流替代变量检验结果——基于信息交易量

注：表中，***、**分别表示1%、5%的显著性水平，括号内数值为相应参数估计的t值。

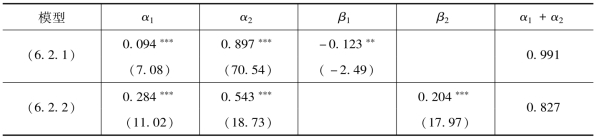
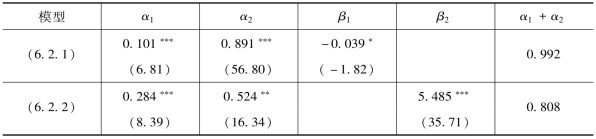
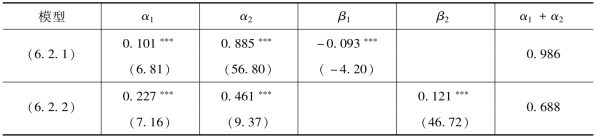
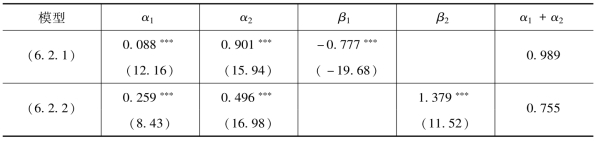
欧洲股票市场上，表6.9、表6.10、表6.11 中，富时100 指数和CAC40 指数、DAX指数的检验结果表明，在GARCH模型的条件方差方程中加入流动性交易量后，持续性参数（α1+α2）分别为0.992、0.986 和0.989，流动性交易量对价格波动的持续性没有明显的影响，并且三个指数流动性交易量系数均显著为负，流动性交易量的产生能够降低市场上的收益波动性。加入信息交易量后，富时100 指数持续性参数（α1+α2）变为0.808，比本章第一节中加入总体交易量时持续性参数为0.836 时略有降低，说明信息交易量也与总体交易量一样，能够部分吸收价格波动的持续性。对于CAC40 指数，在本章第一节的检验结果中，用总体交易量替代信息流变量时对价格的持续性波动基本没有影响。但是，在加入信息交易量以后，代表价格持续性波动的参数（α1+α2）则降低为0.688，说明用信息交易来替代无法被观测的信息流变量更具有合理性。类似地，对于DAX指数，在本章第一节的检验结果中，总体交易量也不能对价格波动的持续性具有一定的解释作用。但在GARCH模型的条件方差方程中加入信息交易量后，发现持续性参数也有一定的降低，变为0.755。三个指数信息交易量与收益波动均同方向变化。

表6.9 富时100 指数信息流替代变量检验结果——基于信息交易量

注：表中，***、**、*分别表示1%、5%、10%的显著性水平，括号内数值为相应参数估计的t值。

表6.10 CAC40 指数信息流替代变量检验结果——基于信息交易量

注：表中，***表示1%的显著性水平，括号内数值为相应参数估计的t值。

表6.11 DAX指数信息流替代变量检验结果——基于信息交易量

(www.xing528.com)

注：表中，***表示1%的显著性水平，括号内数值为相应参数估计的t值。

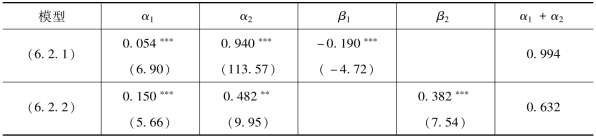
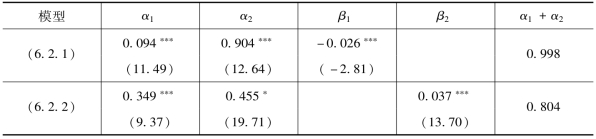
亚洲股票市场上，同样在GARCH模型的条件方差方程中加入流动性交易量时，表6.12、表6.13 和表6.14 中，上证综指、恒生指数、日经225 指数GARCH模型的估计结果表明，持续性参数（α1+α2）分别为0.994、0.998 和0.977，均接近于1 且流动性交易量的系数估计值显著为负值，说明在亚洲股票市场上。类似地，流动性交易量也不能作为信息流的替代变量，但是流动性交易量同样具有降低收益波动的作用。对于上证综指，代表价格持续性波动的参数（α1+α2）在加入信息交易量以后降低为0.632。对于恒生指数和日经225 指数，在6.1 节中基于总体交易量的检验结果显示，总体交易量并不能有效降低价格波动的持续性。但在GARCH模型的条件方差方程中加入信息交易量后发现，恒生指数持续性参数为0.804，日经225 指数为0.728，均有一定程度的降低，说明信息交易量能够部分吸收价格波动的持续性，可以作为信息流的替代变量。同样，三个指数包含信息交易量的GARCH模型估计结果显示，信息交易量的增加能够加剧股票收益的波动，二者同向变动。

表6.12 上证综合指数信息流替代变量检验结果——基于信息交易量

注：表中，***、**分别表示1%、5%的显著性水平，括号内数值为相应参数估计的t值。

表6.13 恒生指数信息流替代变量检验结果——基于信息交易量

注：表中，***、*分别表示1%、10%的显著性水平，括号内数值为相应参数估计的t值。

表6.14日经225 指数信息流替代变量检验结果——基于信息交易量

续表

注：表中，***表示1%的显著性水平，括号内数值为相应参数估计的t值。

综上所述，对于道琼斯指数、富时100 指数、CAC40 指数、DAX指数、上证综指、恒生指数、日经225 指数，模型（6.2.1）和模型（6.2.2）的估计结果表明：

流动性交易量的系数估计值显著为负，说明流动性交易量的增加能够降低股票市场上的收益波动。主要原因在于流动性交易量只是投资者为保持资产流动性或者控制风险而进行的交易，这部分交易量的增加会给信息交易者带来更多的投资对手，增加市场的流动性。因此，流动性交易量的增加应该能够具有降低市场波动的作用。而信息交易量的情况则相反，信息交易量的变化能够带来收益波动的同向变动。

在GARCH模型的条件方差方程中分别加入流动性交易量和信息交易量后发现，流动性交易量并不能明显降低价格波动的持续性。而信息交易量则能够在一定程度上吸收价格波动的持续性。对本节中基于信息交易量的检验结果与本章第一节中基于总体交易量的检验结果进行对比分析，我们会发现：与总体交易量相比较，信息交易量能够更大程度地降低股票价格的持续性波动，作为信息流的代理变量更为合理。异质信念的假设前提下，信息交易可以作为信息流的替代变量。因此，本书第三章第一节中构造的包含异质信念的GARCH模型可以称为一个以信息交易量为混合变量的混合GARCH模型。