股票市场投资者异质信念资产定价理论

传统资产定价理论以投资者同质信念作为假设条件，认为在相同的持有期下，投资者对相同资产的预期收益分布会做出相同的判断。同质信念的假设前提可以概括为：首先，全部信息可以在相同的时间内免费被投资者所接收；其次，投资者采取同样的方式对信息进行处理。显然，同质信念只是一种理想化的假设前提，用异质信念来刻画资本市场上投资者的实际预期更为合理。目前，关于异质信念的研究在理论模型和实证分析方面都取得了一定程度的进展。

Miller（1977）首先指出，投资者异质信念的前提下，卖空限制的存在使得悲观投资者不能充分参与市场中的交易，因此股票价格将主要表现为反映乐观投资者的评价，因此，相对于其真实价值，股票价格将会被高估。投资者异质信念的程度越强，所受卖空限制的程度越严重，股票预期收益越低。

Miller（1977）基于图2-1 形象描述了在股票市场受到卖空限制以及投资者异质信念的假设前提下股票价格的变化过程。

图2-1 异质信念、卖空限制与股票价格

注：图2-1 引自Miller E.，Risk，Uncertainty and Divergence of Opinion，Journal of Finance，1977，32（4）：1151。横轴表示股票的数量，纵轴表示股票的价格。

图2-1 中，曲线ABC可以视为不同价格下，投资者愿意持有的股票份额数即需求曲线，竖直线S1 代表投资者持有的股票份额，为供给曲线。假定每个投资者只能购买的股票份额为一份且共有N份，则均衡状态下的股票价格应为R。假设投资者异质信念的程度增强，曲线ABC变为FBJ，则市场出清价格由R增加为Q。类似的，如果投资者异质信念的程度减弱，曲线ABC变为DBE，出清价格则降低为M。极端的情况下，如果投资者之间不存在异质信念，则曲线ABC变为水平直线GBH，均衡价格为G，只有这种情况下股票价格代表的才是市场中所有投资者的平均估价，这一价格可以视为股票的真实价值。同时，如果考虑卖空，允许卖空的情况下相当于增加市场中股票的供给，供给曲线向右移动，由S1 变为S2。显然，投资者异质信念程度的增强和卖空限制程度的增加都会使得股票价格高于其真实价值。

Harrison 和Kreps（1978）给出了一个简单的例子来描述再售期权的形成机制。假设市场中有两组投资者，分别记为投资者Ⅰ和投资者Ⅱ，他们在每一期所获得的股利为0 或者1，假设a（a =Ⅰ，Ⅱ）组投资者由状态d转换到d′时，估价的概率为qa（d，d′），d，d′∈{0，1}，定义转移矩阵：

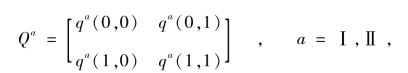
设第Ⅰ组投资者的转换矩阵为，

第Ⅱ组投资者的转换矩阵为，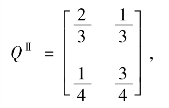

贴现率γ=0.75。定义pa（d）为在d（d =0，1）状态时，投资者a（a =Ⅰ，Ⅱ）对未来股利预期现值的估价，则有：

pⅠ(0)=4/3 =1.33，pⅠ(1)=11/9 =1.22

pⅡ(0)=16/11 =1.45，pⅡ(1)=21/11 =1.91

可见，在两种状态下，第Ⅱ组投资者对未来股利预期现值的估价都要比第Ⅰ组投资者高。我们或许会认为，第Ⅱ组投资者会一直持有股票并且股票在每种状态d 下的价格是pⅡ（d）。如果第Ⅰ组投资者能够预期到这一情形，市场将无法达到均衡状态。为了能够在瞬间转换到状态1 时以1.91的价格卖出股票，投资者Ⅰ会在状态0 时购买股票，这样投资者Ⅰ在状态0 时对未来股利预期现值的估价为：

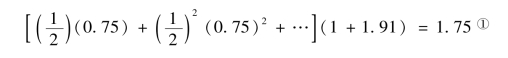
① 具体计算方法参考Harrison 和Kreps（1978）的模型分析。

投资者Ⅰ在状态0 时的估价大于在状态0 时股票的购买价格1.45。因此，如果股票在状态1 时的价格为1.91 或者更高，状态0 时的价格则至少是1.75，这一价格高于投资者Ⅰ在状态0 时的估价，也高于投资者Ⅱ在状态0 时的估价，价格高出的部分主要是因为投资者Ⅰ认为能够在瞬间转换到状态1 时以1.91 的价格卖出股票的预期，这种股票能够以更高价格出售给更乐观投资者的机会价值就是再售期权。

Varian（1985）在假定投资者拥有不同主观概率的前提下对一个Arrow-Debreue模型进行了讨论。在Arrow-Debreue均衡中，资产价格仅依赖于总消费和主观概率的分布。假设在供给固定的情况下，每一个消费因所受限制至多只能购买一单位的资产，且投资者对资产持有不同的保留价格。图2-2 对不同主观概率前提下，均衡价格的变化进行了描述。

图2-2 中，D表示需求曲线，S 为供给曲线，均衡价格为P。如果保留价格变得更加分散，也就是悲观投资者认为资产的价值应该更低，而乐观投资者则认为资产的价值应该更高，此时需求曲线变为D′，均衡价格降低为P′。Varian（1985）进一步指出，如果投资者具有相同的偏好，则只要他们风险规避的程度不会迅速减弱，主观概率分散程度高的资产会具有更低的价格。异质信念程度的增强会带来均衡资产价格的降低，因此投资者异质信念与预期资产收益具有正相关关系。

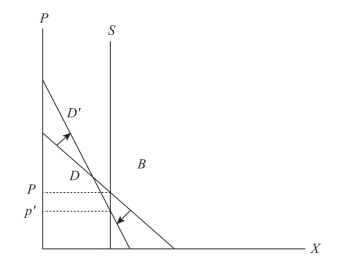
图2-2 异质信念与均衡价格

注：图2-2 引自Varian，H.R.，“ Divergence of Opinion in Complete Markets：A Note”，The Journal of Finance，1985，40（1）：314.横轴表示资产的数量，纵轴表示资产的价格。

Harrison 和Kreps（1978）关于投资者异质信念的研究将投资者视为风险中性的，对风险资产的价值具有异质的预期，并且不能卖空。Morris（1996）考虑了Harrison 和Kreps（1978）所建立模型的一种特殊情形，假定投资者起初对资产基本价值的评价具有差异性，即投资者之间存在“先验的”差异性，但是投资者在不断学习的过程中最终会达成一致的意见，在学习之前即使是轻微的先验性差异也有可能带来大规模的投机溢价（Speculative Premium）。在学习的过程中，如果一个投资者是乐观的，那么在每一期交易之后，他对资产的估价都是最高的。另一方面，如果不存在乐观投资者，那么价格总是会超过每一个投资者的基本估价，但随着时间的推移，价格和投资者的评价最终会趋于客观的基本价值。可见，如果投资者信念的差异性源于先验因素的影响，即使因为再售出期权的原因带来了投机泡沫，投资者也可以在不断学习的基础上预期到真实的资产收益分布情况，这样资产价格会逐渐接近其真实价值。当然，Morris（1996）仅是从先验因素这一角度考虑了异质信念下资产价格与其真实价值的关系，如果同时考虑另外两个因素即渐进的信息传播过程和投资者有限的关注程度，那么相对于真实价值，资产价格可能会有偏离。

Hong和Stein（1999）认为资产市场中有两类不同的交易者，一类是信息交易者（NewsWatchers），另一类是动量交易者（Momentum Traders），这两类交易者都是有限理性的。信息交易者基于观察到的关于未来基本面的信息进行交易，并不考虑当前和过去的价格。而动量交易者则是基于历史交易价格进行交易，因此他们对资产收益的预测只是基于过去历史价格的简单函数。进一步，假定私有信息在信息交易者之间渐进流动。因此，当只有信息交易者参与市场的时候，价格对于新信息的反应较慢，相对于真实价值将是低估的。但如果同时加入动量交易者，由于动量交易者只是基于历史价格进行交易，他们的存在则有可能会使市场达到一种近似有效的状态。但是，当动量交易者试图通过信息交易者对价值的低估来获利的时候，起初价格的反映确实是会向着基本面的方向增加，但同时也会造成价格相对于信息过度反应。例如，在T时刻，假定市场中只有一个好消息，并且消息过后基本面没有发生变化。在T时刻，信息交易者观察到这一利好消息，会使得T+1 期的价格上涨但仍然低于长期的价值，即价格会反应不足（Underreaction）。在T+1 时刻，有一批动量交易者会购买这一资产，此时参与交易的动量交易者会获利，但动量交易者的交易行为同时会导致价格有进一步的增长，这同时又会诱使更多的动量交易者购买该资产，如此下去，最后在某一T+i（i＞1）时刻，由于价格已经超过真实价值，将会导致价格出现过度反应（Overreaction），这一批动量交易者会有所损失。因此，Hong和Stein（1999）从信息渐进传播的角度分析了投资者的交易行为对价格的影响，为价格的持续性动量现象做出了合理的解释。

Hong和Stein（2003）从投资者有限注意这一角度分析了市场崩溃的原因。假定市场中存在两类非完全理性的投资者A和B，A、B两类投资者都从市场中获取股票的私有信息，但是A和B各自只相信自己观察到的信息是最有效的，因此只关注自己的信息，即他们是有限注意的。这样，A和B两类投资者对资产就有不同的估价，因而是异质信念的。除了投资者A和B以外，同时市场中还存在一类完全理性、风险中性的套利者，由于投资者A和B受卖空限制的约束，套利者有时可能并不能观察到他们的估价。假定在第1 期，投资者B得知了一个悲观的信息，那么由于受卖空限制的约束，投资者B将不会参与市场中的交易，整个市场中只有投资者A和套利者之间进行交易。虽然理性套利者此时知道B的估价比A低，但因为B没有参与交易，套利者无法获知具体的估价，因此在1 期，市场价格反映了A的估价但并没有完全反映B在第1 期的估价。如果在第2 期，投资者A得知了一个利好的消息，那么A仍然是乐观的，在第2 期，B在第1 期的悲观信息仍然是被隐藏的。但如果在第2 期，A得知了一个坏消息，此时套利者将会通过观察B是否进入市场来判断第1 期B观察到的信息与第2 期A观察到的信息哪一个更加悲观。只要B仍然未进入市场，套利者就会判断出第1 期B的信息是更悲观的，价格会进一步下降。如果在股价下降的过程中，B能够成为A的边际支持买家，更多的投资者就会了解到他们的信息，不断积累并隐藏的信息有可能会在市场下跌的过程中得以释放，因此可能会带来市场的暴跌甚至是崩溃。

更具体的，设投资者B在第1 期观察到的信息集为SB，且SB～U[0，2V]，投资者A在第2 期观察到的信息集为SA，且SAiid～U[H，2V+H]（其中，H可视为对投资者异质信念的事前度量）。由于套利者是风险中性的，那么第0 期套利者对股票价格的事前预期为，。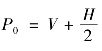

在第1 期，如果仅有的私有信息被B获知，那么会有以下两种情况：第一种情况：如果B的信息被揭露出来，则有，

第二种情况，如果B的信息是隐藏的，即当时，

在第2 期，则可以详细区分为6 种情形，具体的情形，如图2-3所示。

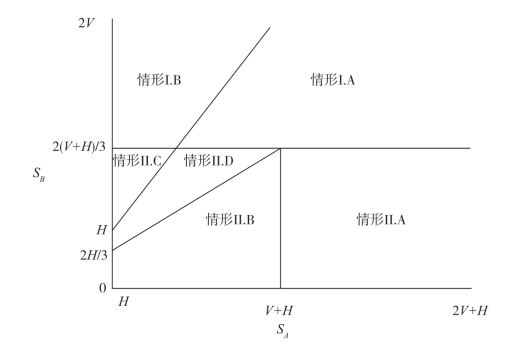
图2-3 投资者A、B的信息被隐藏或者揭露时的六种不同情形

注：图2-3 引自Hong，H.，J.C.Stein，“Differences of Opinion，Short-Sales Constraints and Market Crashes”，The Review of Financial Studies，2003，p501.

图2-3 中的六种情形分别为：

情形Ⅰ.A：SB在第1 期被揭露，SA在第2 期被揭露；

情形Ⅰ.B：SB在第1 期被揭露，SA在第2 期被隐藏；

情形Ⅱ.A：SB在第1 期被隐藏，SA在第2 期被揭露，SB第2 期被隐藏，且；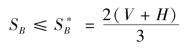

情形Ⅱ.B：SB在第1 期被隐藏，SA在第2 期被揭露，SB在第2 期被隐藏，且；

情形Ⅱ.C：SB在第1 期被隐藏，SA在第1 期被隐藏，SB在第2 期被揭露；

情形Ⅱ.D：SB在第1 期被隐藏，SA和SB在第2 期被揭露。

基于上述六种情况，得出第1 期的均衡价格P1和第2 期的均衡价格P2。因此有从第0 期到第1 期，由于悲观信息在第1 期被隐藏，价格最大可能的上升幅度将大于下降幅度，而从第1 期到第2 期，价格最大可能的下降幅度将大于上升幅度。同时，由于异质信念的存在使得收益序列表出现了不对称的分布特征。在第1 期由于悲观信息被隐藏而出现正偏，在第2 期，如果SB在第1 期是被隐藏的则收益序列负偏，但如果SB在第1 期是被揭露出来，则收益序列有轻微的正偏。异质信念程度越强，SB被隐藏的可能性更大，短期收益更有可能出现负偏。

Scheinkman 和Xiong（2003）给出了一个连续时间的均衡模型，指出由于投资者的过度自信使得投资者对资产基本面的评价产生了意见分歧。

假设存在风险资产，其股利由两部分组成：决定未来股利的基本面因素变量和噪声。股利满足如下过程：

其中，ZD是标准的布朗运动过程，σD是常数波动参数，f是不可观测的基本面因素变量，满足：

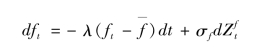
其中，λ≥0 是均值回归参数，f—是f的长期均值，σf＞0 是常数波动参数，Zf是标准的布朗运动过程。

假设有两类风险中性的投资者A和B，他们能观察到信号sA和sB，但是投资者A只将sA视为自己的信号，并认为sA满足如下过程，

类似地，投资者B认为sB满足如下过程，

(www.xing528.com)

可以将φ（0 ＜φ＜1）视为过度自信的参数。

定义gA和gB为异质信念：

均衡资产价格为：

其中，代表其他投资者。

则再售期权的价值为，可以视为执行价格为的看涨期权。可见，在卖空限制的约束下，只要资产购买者认为有比他们更乐观的投资者，便会购买能够向更乐观投资者卖出资产的期权。投资者的出价会高于他们对未来股利的估价，因为他们相信将来能够找到愿意为该资产支付更高价格的购买者。因此，即使在异质信念程度很低时，只要能促成交易，就会给资产价格带来明显的泡沫成分。

基于Scheinkman 和Xiong（2003）关于过度自信是投资者异质信念根源的推断，Hong等（2006）通过建立一个离散时间的多期模型研究了投资者异质信念和卖空限制情况下资产泡沫和投机泡沫之间的关系。假定有两类投资者A和B，在第0 期和第1 期对资产进行交易，第2 期支付股利。

在第0 期，两组投资者对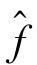持有不同的先验异质信念，分别有，

在第1 期，投资者收到两条公共信息，

那么，第1 期，投资者的异质信念，分别有，

即：

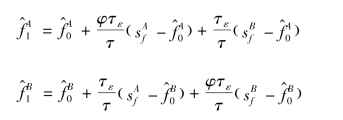
其中，φ可以视为代表投资者过度自信的参数。

异质信念下，第0 期投机泡沫为：其中，Q为流通股份额，用来衡量资产泡沫。

在第一种情况下，投资者A为乐观投资者并在第0 期持有所有的份额。此时泡沫由A、B投资者的初始异质信念以及投资者A对第1 期再售期权的预期价值两部分所决定。

在第二种情况下，第0 期，A、B投资者均选择长期持有股票，因此，泡沫是A、B投资者再售期权的加权平均。

第三种情况与第一种类似，此时投资者B为乐观投资者并在第0 期持有所有的份额，泡沫由A、B投资者的初始异质信念以及投资者B对第1期再售期权的预期价值两部分所决定。

此外，Hong等（2006）还讨论了股票存在锁定期限时的情况，市场中的投资者除了包括A、B投资者（称为外部投资者）外还包括理性的内部投资者（在股票锁定期到期之时，内部投资者可以交易他们持有的股票份额）。此时，由于内部投资者的卖出行为给股票价格带来了更大的投机性成分，因此即使是在投资者提前获知股票锁定期到期日的情况下，股票价格在到期日也会倾向于下跌。Hong等（2006）进一步指出，投资者由于过度自信产生异质信念并受到卖空限制约束的情况下，资产的价格最终会超过其基本价值。首先，由于投资者初始异质信念的差异，在卖空限制的影响下，悲观投资者无法参与交易会导致价格主要表现为乐观投资者的评价，因此价格会升高，这一造成价格上涨的原因被称为“乐观效应”。此外，由于投资者预期到将来会有其他投资者愿意以更高的价格购买他们持有的股票。因此，在前一期投资者会以超出他们对未来股利估价的价格买进股票，导致价格升高，这一造成价格上涨的原因被称为“再售期权效应”。乐观效应与再售期权效应也是投机泡沫产生的原因。股票投机泡沫会伴随资产泡沫的增大而迅速减小，股票换手率和收益波动率也会伴随资产泡沫的增大而减小。

Hong和Stein（2007）对异质信念的形成机制进行了分析，认为投资者的异质信念主要源于信息的“渐进”传播过程、投资者的“有限”关注以及投资者之间存在的“先验”性差异。新信息从产生到被投资者所接收必然会经历一个传播的过程，而信息在传播的过程中又会受到多种不确定性因素影响。市场中的投资者不可能在新信息产生后就立刻接收到这一信息，也不可能在相同的时间里接收到该信息，信息的流动是一个逐步扩散的“渐进”流动过程。因此，投资者之间会因为接收到同一信息时间先后的差异而做出不同的预期，是异质信念的。只要不是处于绝对的封闭状态，投资者每天都会接收到大量的信息。由于精力或者时间以及自身方面（例如过度自信等）的限制他们不可能会去处理所有的信息，只能有选择性地关注比较有价值的或者感兴趣的有限的信息。投资者对信息的这种“有限”关注也是造成他们信念差异的原因。此外，即使投资者之间在获取和关注信息方面并不存在差异，也不可能对资产做出完全相同的预期和评价。投资者在成长环境、受教育经历等方面的差异构成了他们本身固有又很难发生瞬间改变的异质性，这种“先验的”差异性最终会导致投资者对资产做出不同的预期和判断。

此外，Hong和Stein（2007）通过建立一个关于异质信念的模型解释了动量效应和交易量形成的原因。假定有一只股票在第2 期支付清算股利D，D=A+B，其中，A和B是两个独立的零均值正态分布随机变量，也可以看作两个不同信息的期望值。在第0 期，A和B是未知的，因此，此时D的期望值为0。简单起见，假定利率为0，持有股票不存在风险溢价，那么第0 期股票的价格p0也为0。在第1 期，如果有f比例的投资者观察到了信息A，1-f比例的投资者观察到了信息B，并且观察到信息A的投资者错误地认为D=A，观察到信息B的投资者错误的认为D=B，即信息是渐进传播的并且投资者只能注意到有限的信息。在股票供给数量很小，且投资者可以无摩擦地短期或长期持有股票的假设前提下，第1 期股票价格为：

p1=fA+(1-f)B。

从第0 期到第1 期的收益为：R1=P1-P0=fA+（1-f）B，

从第1 期到第2 期的收益为：R2=D-P1=（1-f）A+fB。

用R1和R2的协方差来描述动量，即：M=cov（R1，R2）=f（1-f）（vA+vB），

其中，vA和vB分别是信息A和B的方差。

可以发现，动量通常为正，且在f=（1-f）=1/2 时达到最大。这意味着在第1 期一个正（负）的收益通常会紧接着在2 期也有一个正（负）的收益。此外对于预期交易量（EV），满足：

同样，预期交易量在f=（1-f）=1/2 时达到最大。

显然，如果在第1 期，所有的投资者只关注信息A或者只关注信息B，即f=0 或者f=1，即投资者之间不存在异质信念时，将不会产生交易行为。即使价格相对于基本价值不会发生很大变化，由于异质信念的存在，也会产生大量的交易行为，异质信念促成了大规模交易量的产生。

Xiong和Yan（2009）建立了一个债券市场上两类投资者具有异质信念的动态均衡模型。假设有一类简单的消费品，该消费品的总禀赋满足：

其中，μD和σD是常数，ZD（t）是一个标准的布朗运动过程。假设价格水平pt（例如CPI指数等）满足：

πt是通货膨胀率。πt是一个线性扩散过程，满足：

λπ是均值回归参数，θt为通货膨胀率的长期均值，σπ为波动率参数，Zπ（t）是标准的布朗运动过程且与ZD（t）相互独立。长期均值θt无法观测，服从Ornstein-Uhlenbeck 过程，即：

λθ是均值回归参数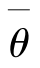，是θt的长期均值，σθ是波动率参数，Zθ（t）是标准的布朗运动过程且与ZD（t）和Zπ（t）相互独立。直观上看，我们可以认为πt是当前的通货膨胀率，θt是不能被公众观测到的货币当局的通胀目标。

假定有两组投资者A和B，在信息集下，投资者对关于通胀目标θt的信息流具有不同的先验认知。

投资者异质信念满足：

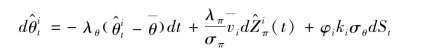
投资者异质信念的前提下，在t时刻，τ年期零息债券的收益为：

可见，异质信念的情况下，债券收益是由投资者的财富加权平均信念决定的。由于正面消息会导致财富由悲观投资者流向乐观投资者，这样就会给乐观投资者一个更大的权重。因此，这种相对财富的变动能够扩大初始信息对债券收益的影响。财富波动能够扩大资产价格的波动，同时也是债券溢价具有时变性的原因。同时Xiong和Yan（2009）进一步指出，由投资者交易行为引起的内生性财富波动能够有效地解决传统代表性代理人模型所面临的诸如债券收益过度波动、预期假说的失效等债券市场上存在的异象。

Banerjee和Kremer（2010）通过建立一个动态异质信念模型分析了异质信念与交易量之间的关系。文章指出，投资者对公众信息的理解存在一定的分歧，投资者的交易行为能够反映出他们之间意见分歧的程度。如果投资者对当前公共信息的理解达成了一致的意见，但对前期信息的理解存在分歧时，Bayesian 修正能使他们的信念趋于一致，我们称这一过程产生的交易量为“信念趋同”交易量。相反，如果投资者在前期具有一致的意见，而当前存在分歧时，相应的交易量则为“异质”交易量。正因为如此，交易量能够反映出投资者信念的变化过程。交易量之间的正相关关系是由于信念趋同交易造成的。当前高程度的异质信念会带来当期的异质性交易和未来的信念趋同交易。当异质信念程度很强时，交易量迅速攀高，伴随着投资者意见的趋同，交易量在将来的时期逐渐回落。因此，异质信念程度较强时交易量会出现聚集和正的相关关系。同样投资者之间的异质信念程度越强，价格的变化幅度也会越大。投资者高程度的意见分歧通常伴随着大规模的交易行为和波动性。

Bloomfield 和Fischer（2010）通过建立一个包含异质信念的世纪迭代模型（Over-Lapping Generation Model，OLG）分析了异质信念与投资成本之间的关系。文章指出投资成本不仅受投资者对公司未来收益的不确定性影响，还受投资者对彼此信念变化的不确定性影响，主要有两种不同类型的异质信念会对投资成本产生影响。一种类型异质信念的产生主要是因为部分投资者认为其他投资者过分依赖于没有信息含量的一些信号。另一种类型异质信念的产生则主要是因为部分投资者认为其他投资者对更多含有信息的信号所给予的关注太少。相对于第一种类型的异质信念而言，第二种类型异质信念存在的情况下，投资者掌握了更多的有效信息，因而能够减小投资的成本。这两种类型异质信念对投资成本的影响主要是由投资者信念的分布和公开信息的特性所决定的。