应用统计调查误差种类：解读应用统计学

统计误差分类如图1.4 所示。

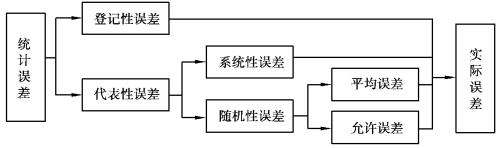
图1.4　统计误差分类图

（1）登记性误差和代表性误差

登记性误差是指统计调查活动过程中由于计量不准确、记录数据出错、抄写过录发生差错、计算过程和结果错误、调查者有意弄虚作假等所造成的误差。

代表性误差是指非全面调查中用部分单位特征推断总体单位特征时，部分单位特征分布不足以代表总体特征分布引起的误差。

（2）系统性误差和随机性误差

系统性误差是指在抽样过程中违反了随机性原则使样本特征分布与总体特征分布不一致产生的误差。

随机性误差是指由于样本做出的估计值随着抽选的样本不同而不同，即使观察完全正确和抽样过程中遵循随机性原则，用样本特征推断总体特征也有的误差。

（3）平均误差和允许误差

平均误差是指在抽样调查估计总体的某个指标值时，当采用一定的抽样方式和选择合适的估计量后，所有可能样本的估计值与总体指标值之间的离差均值。平均误差可以计算，平均数指标抽样平均误差的计算和成数^[4]指标抽样平均误差的计算见表1.5。(www.xing528.com)

表1.5　平均数和成数的平均误差、允许误差、抽样数目计算公式表

允许误差是指样本指标与总体指标之间的抽样误差不超过某一给定的最大可能范围，记为Δ。

式中，t 可通过查表获得，也可用Excel 计算，u 表示抽样平均误差。

允许误差越小，要求的精度就越高，而要达到较高的精度的把握程度就越小，这个把握度称为概率保证度，概率保证度可在（0，1）区间上人为地确定。根据概率保证度查表可求得t（表1.6）。方差S2 代替）；up 表示成数的抽样平均误差；p 表示成数；Δx表示平均数指标抽样的允许误

表1.6　概率保证度与t的对照表

表1.6 中：ux表示平均数的抽样平均误差；σ2 表示总体方差（如果σ2 是未知的，就用样本差；Δp 表示成数指标抽样允许误差。

（4）实际误差

实际误差是指统计调查活动取得调查资料计算的指标与调查总体对应的实际指标真值之间的误差。实际误差不可计算。某一被估计的总体指标值是唯一确定的，然而不同的抽样所得到的样本值却不尽相同，这样抽样实际误差也就成为随机变量，它有不确定的值。而总体指标是未知的，正是需要估计的，因此，抽样实际误差实际上是测定不到的。