空间Durbin计量模型揭示我国区域金融生态效率

传统计量经济学忽视了决策单元的空间依赖性，使得估计结果是有偏的。从空间计量学角度看，地理范围中的经济社会现象或决策单元与近邻地区的决策单元之间是空间自相关的及相互影响的。决策单元的空间效应和空间相关性可用空间误差模型及空间滞后模型进行刻画。不过不同的空间计量模型存在不同的含义，其应用范围也将不同。Le Sage（2009）等通过偏导矩阵定义了空间Durbin模型参数［140］。除因变量外，Durbin模型还考虑了自变量的空间依存性，使其更加符合现实。因变量主要受到来自本地及邻近地区滞后及当期变量的冲击，还来自于其他邻近地区当期和滞后自变量冲击的影响。因此，本文采用空间Durbin计量模型检验我国各省份金融生态运行效率的空间溢出效应，表达式为：

式中，因变量Y表示金融生态运行效率，W表示空间权重矩阵，X为影响金融生态运行效率的因素，WX为金融生态运行效率影响因素滞后项，ε为扰动项。在考虑空间权重矩阵之后，空间计量模型不再具备线性特点，自变量和因变量之间的非线性影响可被回归系数反映。Le Sage等借助偏导矩阵定义了空间Durbin计量模型参数，并给出了空间总效应、空间间接效应及空间直接效应等概念。空间总效应指的是X对所有地区金融生态运行效率造成的平均影响，空间直接效应表示X对本地区金融生态运行效率造成的平均影响，空间间接效应表示X对周边地区金融生态运行效率造成的平均影响。式（7-1）可以进一步改写为式（7-2）：

式（7-2）左右同时乘以（I n-ρW）-1，可表示为：

其中，S r（W）=V（W）（Inβr+Wθr），V（W）=（In-ρW）-1，将式（7-3）展开：

式中，i=1，2，．．．，n，xir表示第i地区第r解释变量的取值情况，S r（W）ij是矩阵S r（W）第i行第j列的元素，V（W）i是矩阵V（W）第i行，式（7-4）与式（7-5），

表征第i地区的自变量X对第i地区金融生态运行效率带来的平均影响，空间直接效应的取值为矩阵Sr（W）对角元素平均值，表示如下：

由式（7-4）和式（7-5），

表示第i地区解释变量X对第j地区金融生态运行效率带来的平均影响，空间间接效应的取值为矩阵Sr（W）中非对角线元素的平均值，如下：(www.xing528.com)

总效应为矩阵Sr（W）所有元素的平均值，表示如下：

其中，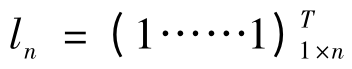

另外，以上计量模型假定了金融生态运行效率不存在时间滞后性。实际上，影响金融生态效率的因素，比如政府干预程度、市场状况等变量无法短期内调整完成，而且金融生态运行效率对于以上变量的敏感程度也决定了滞后效应的大小。所以，本文通过局部调整模型将时间滞后效应纳入空间计量回归模型中。局部调整计量模型如下：

其中，E*表示预期期望的金融生态运行效率值，V由各解释变量向量组成，s为其系数向量，θ为常数项，δ为随机扰动项。式（7-11）表明当期解释变量影响期望的金融生态运行效率值。根据局部调整计量模型的假设，由于市场、政策、技术等内外部条件制约和路径，金融生态运行效率值很难在最短期内调整到期望值，金融生态运行效率的实际变动仅是预期变动的一部分，也就是说存在如下关系：

其中，1-λ（0＜λ＜1）为实际效率向期望效率的调整系数，其值越大表明金融生态运行效率向期望值调整的速度越快。将式（7-12）带入式（7-11）可推出下式：

其中，θ*=（1-λ）θ，s*=（1-λ）s，δ*=（1-λ）δ。s*和s分别表示解释变量V对金融生态运行效率的短期和长期影响；λ为滞后乘数，表示滞后效应的大小，反映前一期金融生态运行效率对当期值的影响。式（7-13）即为本文采取的动态空间面板回归模型。在传统截面空间Durbin计量模型的基础上，Beer等提出了面板空间Durbin计量模型，本文利用Matlab软件及空间计量函数库进行了实证检验。