我国区域金融生态的全局Moran's I指数

全局Moran’s I指数公示如下：

其中：n是样本数据的数量；xi是在变量i在空间的观察值；xi可以变换标准化为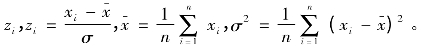进一步可以根据空间数据分别计算出Moran’s I的期望值和期望方差。

对于随机分布假设：

由于原假设没有考虑空间自相关性，通过标准化统计量正态分布表可以做出假设检验：(www.xing528.com)

根据标准化之后的空间权重矩阵，可以计算出全局Moran’s I指数值，Moran’s I数值区间在-1到1之间。［-1，0），0和（0，1］分别表示变量空间负相关，空间不相关以及空间正相关。如果Moran’s I数值为正并通过显著性水平，说明变量在空间分布上是正相关的。也就是在一定地理空间范围之内观测值是相似的；如果Moran’s I数值为负并且通过显著性水平，说明变量在空间分布上是负相关的，即空间范围之内观测值是不相似的。如果Moran’s I数值为零，说明观测值的空间不相关，空间分布是随机的。

利用空间自相关系数可以绘制出Moran’s I散点图，散点图将各地区的金融生态效率评价值划分为四个象限，不同象限代表不同的金融生态效率集聚模式，在此基础上可以识别本地金融生态效率与周边邻近地区金融生态效率之间的空间依存关系。散点图中的第一、第二、第三和第四个象限代表了四种类型的金融生态效率集聚模式：第一象限（H-H）代表高水平金融生态运行效率—高空间滞后，即较高金融生态运行效率的地区与较高金融生态运行效率的地区相邻；第二象限（L-H）代表低水平金融生态运行效率—高空间滞后，即较低金融生态运行效率的地区与较高金融生态运行效率的地区相邻；第三象限（L-L）代表低水平金融生态运行效率—低空间滞后，即较低金融生态运行效率的地区被较低金融生态运行效率的地区相邻；第四象限（H-L）代表为高水平金融生态运行效率—低的空间滞后，即较高金融生态运行效率的地区被较低金融生态运行效率的地区相邻。其中，HH集聚模式和L-L集聚模式均为正的空间自相关，L-H集聚模式和H-L集聚均为负的空间自相关。