(一)相关系数矩阵
使用因子分析法的前提就是各变量之间存在线性相关性,查找相关系数矩阵表可以看出大部分相关系数都超过了0.3,表明主要指标之间存在相关性,可以使用因子分析法。
(二) KMO与Bartlett 球形度检验
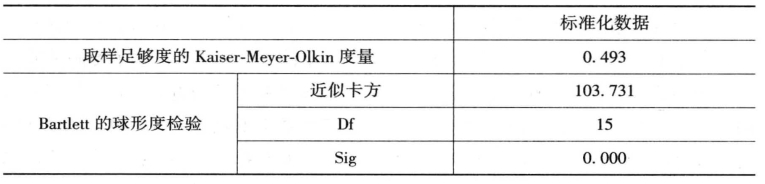
表3-3 是标准化数据的KMO和Bartlett 的检验结果,其中KMO值为0.493,表示应扩充样本;Bartlett 球形检验结果显示,近似卡方较大,且其对应的相伴概率值为0.0 00,远小于显著性水平0.05,表示原变量间存在相关性,拒绝变量独立的假设,认为适合用因子分析法。
表3-3 KMO与Bartlett 的检验
(三)萃取因子
运用主成分分析法对自变量进行公共因子的萃取,以特征值大于1 为萃取条件,并用最大方差法作直交转轴,来决定各变量的因子荷载量。由表3-4 可知,分析后提取出的前五个因子的特征值都是大于1 的,且对总方差的累计贡献均达80%以上。
(四)变量的共同度
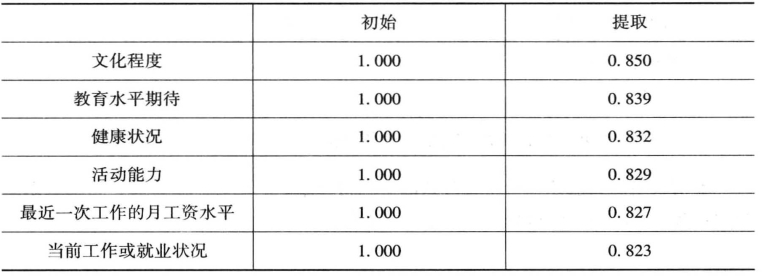
表3- 4是因子分析的初始解,表格中的第二列是根据因子分析初始解得到的变量共同度,变量的共同度均为1,表示原有变量的所有方差都能被因子解释。表格的第三列是在指定条件下(特征根大于1)提取特征根时的共同度,从表中可以发现,公共因子对原始变量的解释程度多在80% 以上,萃取效果明显。(https://www.xing528.com)
表3-4 公因子方差表
(五)因子变量命名
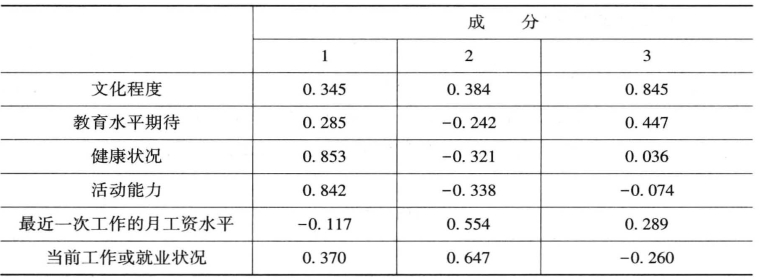
从表3-5 的旋转成分矩阵中,可以发现:
因子1在变量健康状况、活动能力上的系数分别为0.853 和0.842,大于其他变量的系数,主要反映的是健康状况,因此我们将该因子概括为影响健康状况维度因子A。属于家庭禀赋之中的人力资本禀赋部分。
因子2 在最近一次工作的月工资水平和当前工作或就业状况上的系数分别为0.554 和0.647,大于其他变量的系数,反映了家庭的就业能力,因此我们将该因子概括为影响劳动力市场参与状况因子B。稳定的就业和较高的就业能力是实现家庭持续稳定收入的保证,可划分为家庭功能中的家庭保障功能。
因子3 在文化程度、教育水平期待上的系数分别为0.845 和0.447,大于其他变量的系数,都是反映接受教育的情况,因此我们将该因子概括为影响教育投入因子C。教育投资是家庭策略选择中的关键部分,也是家庭支出的重要内容,可认为是家庭策略中的教育投资策略。
表3-5 成分矩阵a
a.已提取了3 个成分。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




