【摘要】:图6.5τ 与St 的关系曲线从图6.5 可看出, 对于静稳定弹箭, 有St <0, τ >1; St→0 时, τ→∞; 对于静不稳定弹箭, 有St >1, 0τ <1。从图6.6 可以看出, 炮弹为了获得陀螺稳定必须满足图6.6静稳定、 陀螺稳定与动稳定之间的关系所以式 是静不稳定弹箭具有动稳定性的必要条件。

为了分析三种稳定性之间的关系, 现在研究动稳定条件中另一个参数τ, 即

如果以St、 τ 为两个笛卡儿坐标参量, 建立直角坐标系, 则τ 与St 的关系如图6.5所示。
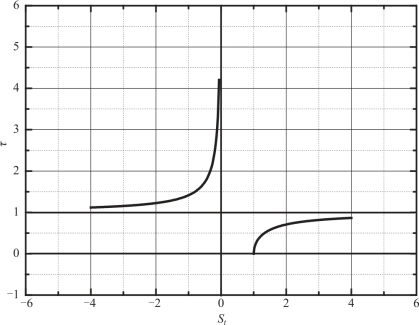
图6.5 τ 与St 的关系曲线
从图6.5 可看出, 对于静稳定弹箭, 有St <0, τ >1; St→0 时, τ→∞; 对于静不稳定弹箭, 有St >1, 0≪τ <1。 利用参数τ 不但可以判别俯仰力矩的特性是起恢复力矩作用还是起翻转力矩作用, 也把静稳定和陀螺稳定的两个条件统一起来。
如果平面Sd、 τ 按静稳定和陀螺稳定来划分, 那么可以很清楚地看出它们与动稳定的关系, 如图6.6 所示在τ =1 直线之上区域为静稳定区域; 在τ =1 直线之下区域为静不稳定区域, 该区域在τ =0 直线之上区域为陀螺稳定区域; 在τ =0 直线之下是陀螺不稳定区域; 显而易见, 动稳定区域仅是陀螺稳定区域中的小部分。(https://www.xing528.com)
从图6.6 可以看出, 炮弹为了获得陀螺稳定必须满足

图6.6 静稳定、 陀螺稳定与动稳定之间的关系
![]()
所以式(6.43) 是静不稳定弹箭具有动稳定性的必要条件。
如果静稳定的弹箭满足式(6.43), 则它肯定是动稳定的, 且和τ 的取值无关, 即式(6.43) 是静稳定弹箭具有动稳定性的充分条件。
在线性气动力、 力矩作用下, 弹箭具有动稳定的充要条件, 即
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




