采用管式发射的卷弧尾翼弹箭在发射前， 卷弧尾翼能够方便地贴附于弹体表面， 不占用弹体内部空间， 为尾喷管和内部器件留出安放空间。 发射后， 卷弧尾翼展开， 为弹体提供稳定和滚转力矩。 卷弧尾翼这种方便卷包的特点为管式发射弹箭的发射与储存提供了方便。 对于卷弧尾翼特殊的空间卷曲， 以及非面对称布局形式， 不但具有特殊的自诱导滚转力矩， 而且会诱导出远超出具有相同投影形状平板尾翼的面外力和面外力矩。
为了方便对比， 同时计算了卷弧尾翼外形与平板尾翼外形两个模型（图5.20）。 平板尾翼外形与卷弧尾翼的投影形状相同。 两个外形的弹径为d， 弹体长度为25d， 采用了6 片尾翼， 其安装角均为0.5°， 尾翼圆心角为60°， 尾翼张开角为90°。
图5.20 卷弧尾翼外形与平板尾翼外形
（a） 卷弧尾翼外形模型； （b） 平板尾翼外形模型； （c） 卷弧尾翼； （d） 平板尾翼
5.3.2.1 卷弧尾翼面外力和力矩生成机理分析
为了研究卷弧尾翼的面外力和力矩生成的机理， 对比分析了卷弧尾翼和平板尾翼的尾翼区域的流动特点。 考虑到弹体的转动频率远大于其攻角的变化频率， 弹体的角运动主要受到尾翼旋转过程所引起的时均气动特性影响， 而难以响应旋转运动所引起的瞬时气动特性。 也就是说， 对弹体的攻角运动有贡献的主要体现在时均面外力和力矩方面。而翼身组合体中， 尾翼对面外力和力矩的贡献是主要的， 因此对卷弧尾翼外形和平板尾翼外形的尾翼区域流场进行了时均化处理。
定义
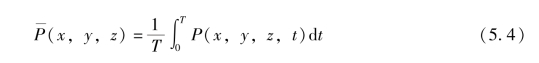
式中， T 为弹体的旋转运动周期。
图5.21 所示为马赫数Ma∞＝4.5、 攻角α ＝2°、 无量纲转速
＝0.018 时， 卷弧尾翼和平板尾翼区域流场时均化后的激波分布图。 由图可以看出， 由于气流经过翼前缘后形成了激波， 相邻翼片以形成的激波向后发展， 在翼间形成交汇。 对比卷弧尾翼和平板尾翼， 卷弧尾翼由于空间卷曲， 凸面将激波向凹面挤压。 因此， 两股激波交汇后， 形成的高压区域并不在翼片间的中心位置， 而更加偏向于凹面， 远离凸面。 另外， 由于卷弧尾翼的卷曲将会使高压流动容易被包裹在翼间区域， 而平板尾翼相邻两片翼之间形成的激波位移比较对称， 两道激波形成的交汇基本位于翼间的中心区域， 而且激波也更容易离开翼间的区域。
图5.21 尾翼区的激波分布图（Ma∞＝4.5， α ＝2°）
（a） 卷弧尾翼； （b） 平板尾翼
由于卷弧尾翼和平板尾翼区的流动特性差异， 导致两者在尾翼间的压力分布也有明显的区别。 如图5.22 所示， 两种尾翼由于激波的作用都在尾翼区域形成了倒Y 字形的高压区。 但是， 两种尾翼存在明显区别， 平板尾翼形成的高压区强度明显弱于卷弧尾翼形成的高压区强度， 而且平板尾翼形成的倒Y 字形比较对称。 卷弧尾翼形成的倒Y 字形更靠近卷弧尾翼的凹面， 并且该部分的压力大。
图5.22 尾翼区域的压力分布图（Ma∞＝4.5， α ＝2°）
（a） 卷弧尾翼； （b） 平板尾翼
图5.23 所示为卷弧尾翼和平板尾翼间弹身上的压力分布曲线。 由图可以看出， 两种翼区的转动去向侧的压力都较转动来向侧的压力大。 相对于平板尾翼， 卷弧尾翼由于其展向的卷曲， 将会使高压气流更多地向凹面靠近， 卷弧尾翼的凹面将高压气流更长时间地包裹在其腔内， 从而靠近凹面的压力明显大于凸面的压力。 对比两种尾翼三个截面凹面和凸面的压力差， 卷弧尾翼的三个截面处的压力差分别为21 691Pa、 15 083Pa、7 669Pa， 而平板尾翼三个截面处的压力差分别为13 737Pa、 5 043Pa、 2 459Pa。 卷弧尾翼外形三个截面处两端的压力差分别是平板尾翼外形的1.6 倍、 3.0 倍和3.1 倍。 由此可以看出， 卷弧尾翼的卷曲效应使得其中段和尾段包裹了更多的高压气流。 这些高压气流会作用在翼面上， 使得卷弧尾翼凹面和凸面的压力出现明显的差距， 从而诱导出数倍于平板尾翼的面外力。
图5.23 尾翼区域弹身的压力分布图（Ma∞＝4.5， α ＝2°）
（a） 卷弧尾翼； （b） 平板尾翼
考虑到尾翼的转动过程的流动呈现较强的非定常性， 而对于弹体的攻角运动存在明显影响的主要是其时均气动力， 因此这里先对尾翼的压力系数进行时均化处理， 定义
式中， nz 为翼面法向在z 方向的分量。
图5.24 所示为卷弧尾翼和平板尾翼两面的Cpz分布云图。 由图可以看出， 由于卷弧尾翼凸面和凹面的Cpz分布不仅方向相反， 而且量值的分布也明显不对称， 这主要是受翼面间的高压分布向凹面靠近的影响， 凹面上的Cpz较凸面的更大。 相比较而言， 平板尾翼两侧的Cpz分布基本是对称的， 仅仅是受力的方向相反。
图5.24 翼面压力系数z 向投影分布图（Ma∞＝4.5， α ＝2°）
（a） 卷弧尾翼； （b） 平板尾翼
图5.25 所示为卷弧尾翼和平板尾翼上三个截面的Cpz分布曲线， 尾翼两侧Cpz的积分即为马格努斯力。 由图可以看出， 平板尾翼三个截面上两侧的Cpz基本是对称的； 而卷弧尾翼两侧的Cpz却存在较大差别， 凹面的Cpz较凸面的大， 而且沿弦向后移， 凸面的Cpz逐渐增大， 特别是在翼梢区域， Cpz逐渐变为正值。 由卷弧尾翼截面上的Cpz分布曲线可以看出， 由于卷弧尾翼的卷曲效应， 使得其两侧的Cpz分布不对称， 因此会引起数倍于平板尾翼的面外力和力矩。
图5.25 翼面上三个截面的Cpz曲线（Ma∞＝4.5， α ＝2°）
（a） 卷弧尾翼； （b） 平板尾翼
5.3.2.2 气动特性随攻角和马赫数的变化规律
图5.26 所示为卷弧尾翼和平板尾翼外形的时均俯仰力矩系数随攻角的变化曲线。由图可以看出， 由于两种外形的尾翼的投影形状和面积相同， 因此其俯仰力矩系数基本相同。 另外， 由图还可以看出， 随着马赫数增加， 两种外形的俯仰力矩系数随攻角变化曲线的斜率在减小， 也就是说两种外形尾翼的纵向静稳定能力随着马赫数增大而下降。
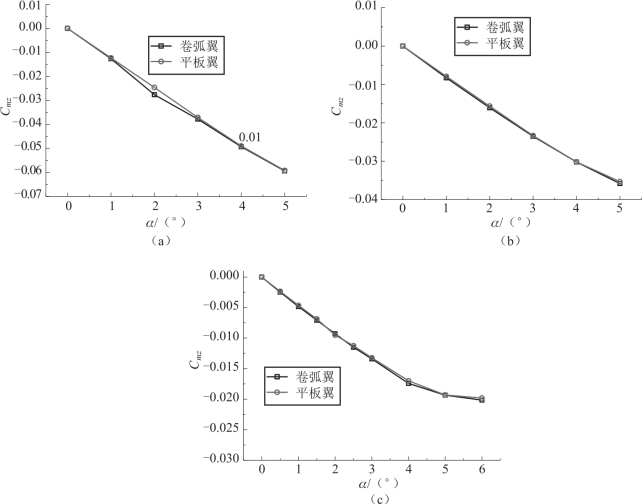
图5.26 卷弧尾翼和平板尾翼火箭弹俯仰力矩系数随攻角的变化曲线
（a） Ma∞＝3.5； （b） Ma∞＝4.0； （c） Ma∞＝4.5
图5.27 所示为两种外形尾翼的马格努斯力矩系数对攻角的导数随攻角的变化曲线。由图可以看出， 卷弧尾翼的马格努斯力矩系数导数数倍于平板尾翼的马格努斯力矩系数导数。 而且对比三个马赫数下的马格努斯力系数可以发现， 随着马赫数增大， 平板尾翼的下降趋势明显大于卷弧尾翼。 因此， 在高马赫数时， 两者相差的倍数更多。 另外， 两种外形即便在小攻角下， 马格努斯力矩系数也将是非线性变化。 马格努斯力矩使弹体偏离攻角平面为不稳定力矩， 卷弧尾翼的马格努斯力矩系数数倍于平板尾翼， 将更容易出现锥形运动失稳。
5.3.2.3 尾翼数量和旋转方向的影响
图5.28 所示为6 片、 4 片卷弧尾翼与平板尾翼外形单片翼的马格努斯力矩系数随滚转角的变化曲线， 以及各曲线的时均值。 表5.2 给出了马赫数Ma∞＝4.5 时， 卷弧尾翼外形的尾翼数量、 正转与反转对全弹和一片尾翼马格努斯力矩系数的时均值。 表中正、 反表示转速指向x 轴正向或负向。
图5.27 两外形时均马格努斯力矩系数对攻角的导数变化曲线
（a） Ma∞＝3.5； （b） Ma∞＝4.0； （c） Ma∞＝4.5
图5.28 组合体外形中单片卷弧尾翼与平板尾翼马格努斯力矩系数对比
（Ma∞＝4.5， 
＝0.008 9， α ＝2°， 
＝0.008 9）(www.xing528.com)
表5.2 单片尾翼的时均值面外力矩系数导数
（Ma∞＝4.5， 
＝0.008 9）
由此可以看出， 单片尾翼的马格努斯力矩系数在一个滚转周期内出现了多次波动。一片卷弧翼的马格努斯力矩系数明显大于平板翼。 6 片卷弧尾翼外形的单片尾翼产生的马格努斯力矩也稍大于4 片卷弧尾翼外形的单片翼， 即增加尾翼数量会加剧尾翼之间的干扰， 使得每片尾翼的马格努斯力矩增加。 由于转速较低， 所以旋转效应对马格努斯力矩的贡献量也非常有限， 主要还是由外形非对称性造成。 卷弧尾翼火箭正转和反转引起的马格努斯力矩相近。
5.3.2.4 卷弧翼张开角的影响
卷弧尾翼和平板尾翼外形的马格努斯力矩特性有明显的差距， 造成这种差距的本质原因在于尾翼的形状。 为了在保证尾翼为卷弧结构的基础上， 通过一定的外形优化以减小马格努斯力矩特性， 首先定义卷弧尾翼的张开角和圆心角。 如图5.29 所示， θ0 为翼面圆心角， 表示卷弧翼凹面的圆心分别与翼根翼梢连线的夹角； θ1 为翼片张开角， 表示卷弧翼翼根与凹面的圆心连线与翼根与弹身圆心连线的夹角。 下面分别研究圆心角与张开角变化对马格努斯力矩系数的影响， 在进行圆心角变化和张开角变化时， 尾翼的展长不变， 即尾翼的投影形状和面积不变， 以保证外形的俯仰力矩系数不会发生改变。
将圆心角固定为θ0 ＝68°， 计算不同张开角卷弧尾翼外形的马格努斯力矩系数（图5.30）。 图5.31 给出了Ma∞＝4.5 时， 卷弧尾翼外形全弹、 尾翼部分、 后体弹身部分的马格努斯力矩系数随尾翼张开角的变化曲线。 由图可以看出， 随着尾翼张开角的增大，尾翼部分和后体弹身部分的马格努斯力矩系数呈现减小的趋势， 而前体弹身部分对马格努斯力矩的贡献可以忽略， 所以全弹马格努斯力矩系数有减小的趋势。 值得注意的是，张开角θ1 ＝115°和θ1 ＝130°时， 后体弹身部分和尾翼部分的马格努斯力矩发生换向。 但是量值接近， 所以全弹的马格努斯力矩基本保持不变。 总之， 保持固定的尾翼的圆心角时， 增大张开角可以减小后体弹身和尾翼部分的马格努斯力矩。
图5.29 卷弧尾翼圆心角和张开角示意图
图5.30 不同张开角外形横截面示意图
5.3.2.5 卷弧尾翼圆心角的影响
将翼片张开角固定为θ1 ＝90°， 分析圆心角对尾翼马格努斯力矩系数的影响。 图5.32 所示为Ma∞＝4.5 时， 卷弧尾翼火箭全弹、 尾翼部分、 后体弹身部分的马格努斯力矩系数随尾翼圆心角的变化曲线。 可以看出， 随着尾翼圆心角的增大， 尾翼部分和后体弹身部分的马格努斯力矩系数绝对值增大。 就增幅而言， 后体弹身部分的马格努斯力矩系数的增幅更为明显， 所以导致全弹正y 方向马格努斯力矩系数增大。 总之， 增加卷弧尾翼的曲率会增大全弹马格努斯力矩。
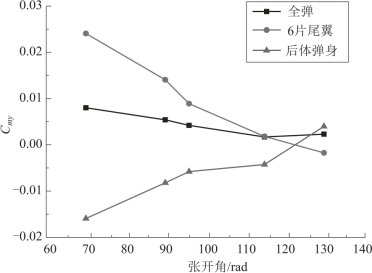
图5.31 马格努斯力矩系数随尾翼张开角的变化曲线
（Ma∞＝4.5， 
＝0.008 9， α ＝2°）
图5.32 马格努斯力矩系数随尾翼圆心角的变化曲线
（Ma∞＝4.5， 
＝0.008 9， α ＝2°）
图5.33 所示为不同卷弧尾翼圆心角， 后体弹身和尾翼表面压力分布云图。 由图可以看出， 随着尾翼圆心角的增大， 尾翼前缘激波相交在弹体上产生的高压区范围增大，而且高压量值增大。 同样， 激波对相邻尾翼翼根和后缘的干扰增强。
图5.34 所示为Ma∞＝4.0、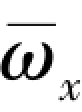 
＝0.007 5、 α ＝2°和不同尾翼圆心角时， 后体弹身和尾翼区总法向力、 马格努斯力系数沿翼根弦的分布曲线。 由图可以看出， 法向力系数随着尾翼圆心角的增大而增大， 但量值的变化很小。 然而， 马格努斯力随着圆心角的增大有着明显的增大， 特别是在尾翼前缘至2/3 弦长位置区域。
图5.33 不同圆心角时后体弹身和尾翼区压力分布云图
（a） θ0 ＝14°； （b） θ0 ＝47°； （c） θ0 ＝56°； （d） θ0 ＝68°
（Ma∞＝4.5， 
＝0.008 9， α ＝2°）
图5.34 尾翼气动力系数沿翼根弦的分布曲线
（a） 法向力系数； （b） 马格努斯力系数
（Ma∞＝4.0，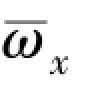 
＝0.007 5， α ＝2°）
5.3.2.6 前缘后掠角的影响
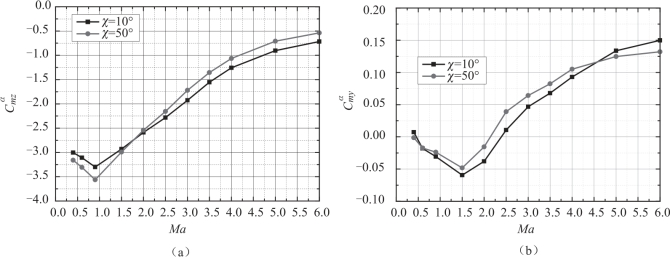
图5.35 不同后掠角气动系数随马赫数的变化
（a） 俯仰力矩系数导数； （b） 马格努斯力矩系数导数
5.3.2.7 弹身长径比对卷弧尾翼外形气动特性的影响
弹箭采用加长发动机的方式增加射程， 会使得弹体的长径比增加。 理论分析表明，单独弹身的马格努斯力系数对攻角和转速的导数与弹身长径比成二次方关系。 但是， 有关卷弧尾翼－弹身组合体的长径比对马格努斯力系数的影响还没有明确的结论。 下面分析卷弧尾翼弹身组合体的长径比对马格努斯力和法向力特性的影响。
图5.36 三个长径比弹身外形图
（a） L/d ＝15； （b） L/d ＝20； （c） L/d ＝25
采用数值模拟方法分别计算了弹身长径比L/d 为15、 20 和25 的卷弧尾翼弹身组合体的气动特性。 三个长径比外形的弹身头部与尾翼的外形和尺寸都相同， 仅通过改变弹身中段的长度得到不同的长径比（图5.36）。 图5.37 所示为马赫数Ma∞＝4.5， 攻角α ＝4°时， 弹身的时均气动力系数沿弹轴的分布曲线。 由图5.37 （a） 可以看出， 弹身长径比的变化对于法向力系数的分布影响并不明显。 但由图5.37 （b） 可以看出， 弹身长径比增加使得弹身段和尾翼段的马格努斯力系数都增大。 如果三个长径比弹体的质心位置都为
cg ＝0.4， 由沿x 轴积分可知， 长径比由15 增至25， 使全弹时均俯仰力矩系数增大约3.4%， 时均马格努斯力矩系数增大约52.9%。 由于弹箭的长径比增加主要是增加发动机的长度， 如果将发动机工作后质心的前移量考虑进去， 长径比增加导致的马格努斯力矩系数增加量将更为显著。
图5.37 弹体时均气动力系数沿弹轴的分布曲线（Ma∞＝4.5， α ＝4°）
（a） 法向力系数导数； （b 马格努斯力系数
5.3.2.8 卷弧尾翼展弦比对气动特性的影响
与卷弧尾翼相比， 平板尾翼拥有较小的马格努斯力矩。 从外形优化设计的角度出发， 一方面可以考虑增大尾翼曲率半径， 即越类似于平板尾翼越好； 另一方面可以调整尾翼展弦比， 以减小翼身和尾翼之间的干扰效应。 以下将在卷弧尾翼投影面积不变的基础上， 改变展弦比来调整卷弧尾翼的气动特性。 以长径比L/d ＝25 的弹体为基础， 设计了尾翼半展弦比λ′＝0.34、 0.30 和0.28 （半展弦比为单片尾翼的展长除以等效弦长）三种尾翼外形（图5.38）。 尾翼展弦比的调整是通过增加弦长、 减小展长实现的， 不同展弦比尾翼的曲率和前后缘后掠角都相同。
图5.38 三种展弦比尾翼外形示意图
采用数值模拟方法对三种外形进行了数值模拟， 图5.39 给出了三种展弦比卷弧尾翼外形时均俯仰力矩系数对攻角导数与马格努斯力矩系数对攻角导数随马赫数变化曲线。 由图可以看出， 俯仰力矩系数导数随马赫数增大而减小。 而且虽然三个尾翼的投影面积相同， 但是展弦比大的尾翼外形其俯仰力矩系数导数还是要大于展弦比小的尾翼外形的俯仰力矩系数导数。 展弦比由λ′＝0.28 增至λ′＝0.34， 俯仰力矩系数导数增大约13%。 而展弦比对马格努斯力矩系数导数的影响却非常明显， 展弦比由λ′＝0.34 减小至λ′＝0.28， 马格努斯力矩系数导数减小了约50%。 这是因为展弦比增大， 卷弧尾翼对其前缘产生激波的“聚拢” 效应增强， 同时对弹身干扰效应增强。
图5.39 气动系数导数随马赫数的变化曲线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
