雷诺数影响弹身马格努斯力系数的研究成果

在大攻角和足够小雷诺数以及转速下， 边界层为层流， 但背风面出现分离。 随着旋转运动的加入， 分离涡开始向旋转方向偏转。 顺着旋转方向的涡向弹身靠近， 而反旋转方向的涡的分离点向旋转方向偏转。 在大攻角下， 分离流在流动中占主导， 提供与经典马格努斯力方向相反的力（图5.7）。

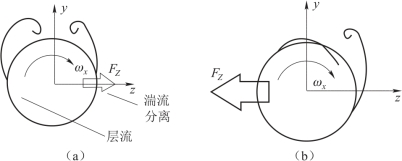
图5.7　大攻角下旋转弹身的分离涡模式

（a） 低转速； （b） 高转速

虽然旋转弹箭在一定攻角下的横向流动不能完全等效为绕二维圆柱的流动， 但是为了简单阐述大攻角下旋转弹身产生的负马格努斯力， 常常以旋转二维圆柱绕流为例进行解释。 对于不旋转的圆柱， 随着雷诺数达到临界值， 在圆柱横截面周向角约为82°处开始出现层流分离。 随着雷诺数继续增加， 边界层开始变为湍流， 分离点向下游背风面移动到130°左右。 对于旋转弹身， 当雷诺数接近临界值时， 分离点也受到非常大的影响， 如图5.8 所示。 在旋转方向与来流方向相反的一侧具有更大的相对速度， 进而引起湍流分离； 在旋转方向与来流方向相同一侧的相对速度更小， 因此为层流分离； 在旋转方向与流动方向相同的一侧分离发生了延迟， 压力较低， 进而产生了马格努斯力。

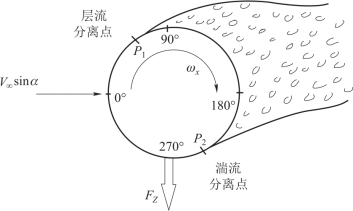
图5.8　临界雷诺数附近旋转二维圆柱绕流示意图

旋转弹身背风面的分离模式对弹身的马格努斯力影响很大， 甚至可以改变马格努斯力的方向。 影响绕弹身流动体涡分离模式的主要因素包括攻角、 转速、 横流雷诺数等。这些因素对马格努斯力的影响是相互交联的， 将攻角的影响考虑在内的横流雷诺数定义为(www.xing528.com)

当横流雷诺数Recf小于临界值时， 马格努斯力受攻角的影响显著； 而当横流雷诺数Recf超过临界值后， 马格努斯力对攻角的变化不再敏感。

图5.9 所示为Seginer[4]给出的弹身在不同横流雷诺数下随攻角和转速变化的试验结果。 试验来流马赫数Ma∞＝0.1， 雷诺数Re∞＝8 ×104。 当横流雷诺数Recf≤5.14 ×104 时， 马格努斯力随攻角增大而增大。 当攻角α<20°时， 在相同攻角下， 马格努斯力随转速的增大呈现剧烈变化。 而当转速增大到一定程度后， 马格努斯力随转速的增大出现比较平缓的变化。 当攻角α>20°， 马格努斯力随转速的增大而继续增大。

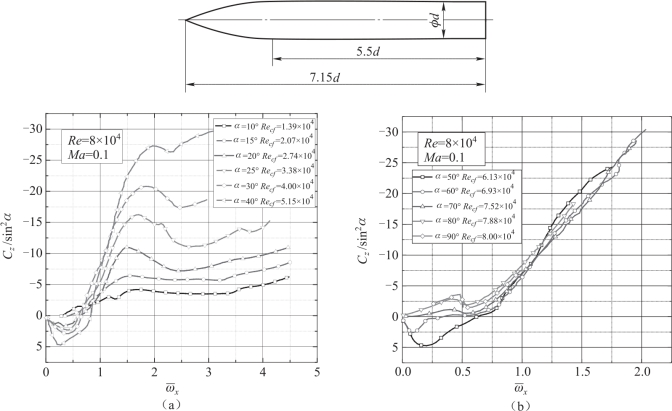
图5.9　马格努斯力随攻角转速变化曲线[4]

（a） Recf≤5.14 ×104； （b） Recf >5.14 ×104
（Ma∞＝0.1， Re∞＝8 ×104）

横流雷诺数Recf >5.14 ×104 时， 在转速较小时马格努斯力随攻角的增大而剧烈变化。 转速增大到一定程度后， 马格努斯力不再随攻角发生明显变化， 而随转速的增大近似呈线性增大。 由图5.9 也可以看出， 攻角α 在20° ~60°范围内转速不太大时， 弹身的马格努斯力与经典马格努斯力方向相反。