弹身马格努斯力系数横流比拟参数的研究结果

由图5.1 可以看出， 弹身的马格努斯力是弹身长径比的函数。 由风洞试验结果得知， 弹身的马格努斯力系数也是攻角、 转速以及雷诺数等参数的函数， 而且在亚声速时， 弹身的马格努斯力系数变化更为复杂。 为了简化数据， 便于更一般性的规律分析，给出了横流比拟参数Cs 的定义为

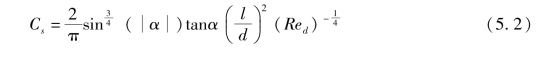
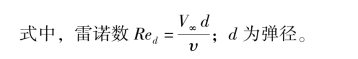
图5.4 以横流比拟参数Cs 为横坐标重新绘制了图5.1 的试验数据， 以及另一个长径比l/d ＝7 的弹身在亚声速下马格努斯力系数的试验数据[3]。 由图可以看出， 横坐标采用横流比拟参数后， 各组的马格努斯力系数数据基本都相互靠拢。 表明以组合量横流比拟参数对不同长径比的弹身， 在不同攻角、 不同马赫数、 不同雷诺数下的马格努斯力系数进行拟合是可行的。 另外还发现， 对于长径比大的弹身， 采用横流比拟参数的效果较好； 对于长径比小的弹身则偏差较大。 这主要是由于长径比小的弹身， 马格努斯力的贡献主要是由边界层位移厚度畸变导致的， 与横流分离涡关系不大。

图5.4　马格努斯力系数随横流比拟参数的变化曲线（亚/跨声速）

（a） 0.1≤Ma∞≤0.16； （b） 0.291≤Ma∞≤0.914(www.xing528.com)

图5.5 给出超声速下， 以横流比拟参数Cs 为横坐标的多个弹身的风洞试验数据。由图可以看出， 超声速下以横流比拟参数Cs 对弹身的马格努斯力系数进行归一化处理效果更好。

采用横流比拟参数来拟合亚声速时， 弹身的马格努斯力系数随速度、 攻角、 转速、长径比等参数的变化， 尽管与一些文献给出的气动数据在数值上不完全吻合， 但是马格努斯力系数随横流比拟参数的变化规律基本是一致的。

在亚声速时， 当转速 增大到一定程度后， 马格努斯系数导数随转速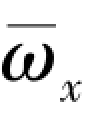的增大而降低。 图5.6 给出了长径比l/d ＝7 的弹身， 在马赫数Ma∞＝0.291 时， 不同攻角下， 马格努斯力系数随组合参数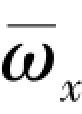Cs 的变化曲线。 由图可以看出， 组合参数很好地拟合了马格努斯力系数的线性部分。 但在各攻角下， 马格努斯力系数随转速增大到一定程度后， 都会进入变化缓慢区域。 而攻角越大， 进入该区域的转速也越大。 进入变化缓慢区域后， 马格努斯力系数对转速的导数逐渐减小。 因此马格努斯力系数对转速的导数随转速是非线性变化的。

图5.5　马格努斯力系数随横流比拟参数的变化曲线（超声速）

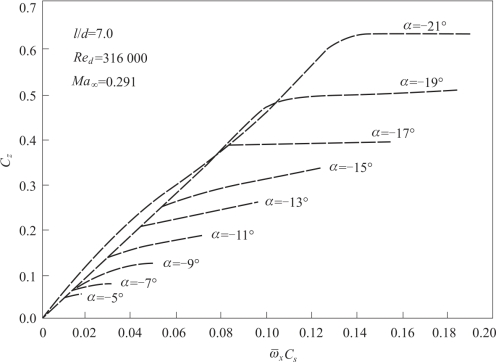
图5.6　单独弹身马格努斯力系数随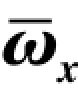Cs 变化曲线