弹箭旋转空气动力效应的数值模拟

为了对比谐波平衡法与非定常N－S 方程双时间步法对旋转空气动力效应的模拟能力， 分别采用双时间步法结合滑移网格技术， 以及谐波平衡法计算了ANF 尾翼－弹身组合体外形的旋转绕流场， 并将得到的气动数据与试验数据[11]进行对比。 两种方法中都采用了SA－DES 方法模拟湍流。 图4.46 为ANF 模型， 其中长度都用弹径d 无量纲化， 弹体长为10d， 尾翼展长为3d。 计算模型采用了贴体结构化网格（图4.47）， 弹体轴向网格数为142， 周向为152， 总网格数为410 万， y ＋<1。 计算马赫数Ma∞＝2.5，攻角α ＝20°， 转速ωx ＝257.23 rad/s， Re ＝1.86 ×105。 参考长度为弹径d， 参考面积为弹身横截面积。

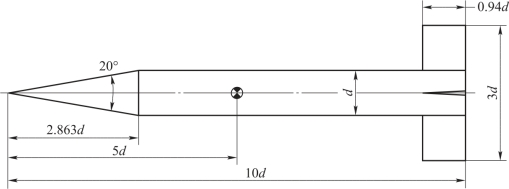
图4.46　ANF 尾翼弹身组合体外形示意图

图4.47　谐波平衡法的计算网格

（a） 计算域网格分布； （b） 飞行器附近的网格分布

双时间步法中， 物理时间步长Δτ ＝3 ×10 －5 s， 每物理时间步迭代30 次。 谐波平衡法中， 谐波数会显著影响计算速度、 计算精度以及内存占用量。 综合精度与计算需求，选取4 谐波、 8 谐波、 10 谐波三种谐波数进行计算。

图4.48 所示为双时间步法和谐波平衡法的气动系数随滚转角的变化曲线。 由图可以看出， 当谐波数为4 时， 谐波平衡法和双时间步法的气动系数曲线区别较大。 当谐波数为8 时， 谐波平衡法已经可以得到接近于双时间步法的气动系数曲线。 但是， 气动系数曲线的细节仍然存在区别。 当谐波数达到10 时， 法向力系数曲线和俯仰力矩系数曲线的波形细节也可以被算出， 并且马格努斯力系数和马格努斯力矩系数在波峰与波谷处的变化曲线也与双时间步法得到的值吻合较好。

表4.2 给出了双时间步法、 谐波平衡法和风洞试验气动系数时均值。 由表可以看出， 当谐波数为4 时， 谐波平衡法和双时间步法的气动系数时均值的差距小于12.5%。谐波数增加时， 谐波平衡法和双时间步法的计算结果的差距迅速减小。 当谐波数为10时， 谐波平衡法和双时间步法的马格努斯力系数和马格努斯力矩系数时均值相对差为3% ~6%， 而法向力系数和俯仰力矩系数的相对差小于1%。 因此， 谐波数为10 时谐波平衡法已经可以给出较为准确的模拟AFN 尾翼－弹身组合体的马格努斯力和力矩系数。(https://www.xing528.com)

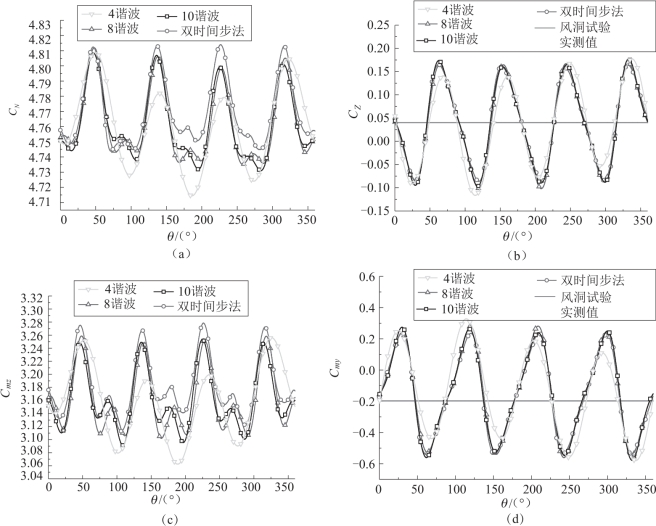
图4.48　双时间步法和谐波平衡法的气动系数随滚转角的变化曲线

（a） 法向力系数； （b） 马格努斯力系数； （c） 俯仰力矩系数； （d） 马格努斯力矩系数
（Ma∞＝2.5， α ＝20°， ωx ＝257.23rad/s， Re ＝1.86 ×105）

表4.2　双时间步法、 谐波平衡法和风洞试验的气动系数时均值

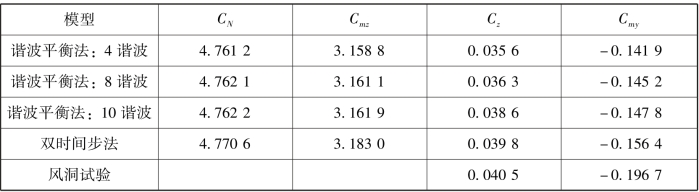
图4.49 所示为采用谐波平衡法在谐波数为4、 10 时， 以及由双时间步法计算得到的弹体背风面压力分布和尾翼处横截面速度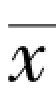（＝0.45） 分布云图。 由图可以看出， 当谐波数为4 时， 谐波平衡法计算得到的流场与双时间步法差别较大。 而谐波数为10 的计算结果与双时间步法吻合较好。 由此可知， 当谐波数足够多时， 谐波平衡法也可以准确模拟旋转尾翼－弹身组合体的绕流场。 但在流动变化剧烈的区域（如大攻角下的弹体背风区）， 得到的流场精度还与双时间步法有差距。

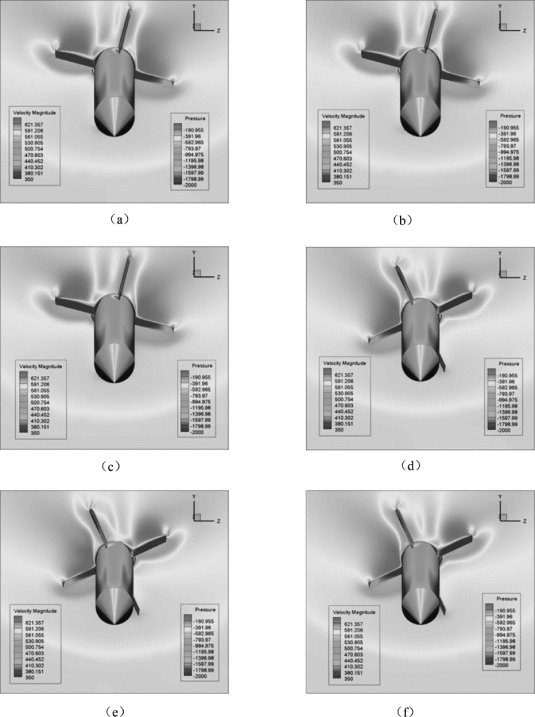
图4.49　弹体压力分布与横截面速度分布云图

（a） 谐波平衡法（谐波数为4， θ ＝120°）； （b） 谐波平衡法（谐波数为10， θ ＝120°）；
（c） 双时间步法（θ ＝120°）； （d） 谐波平衡法（谐波数为4， θ ＝160°）；
（e） 谐波平衡法（谐波数为10， θ ＝160°）； （f） 双时间步法（θ ＝160°）
（Ma∞＝2.5， α ＝20°， ωx ＝257.23rad/s， Re ＝1.86 ×105）