弹箭旋转空气动力效应数值模拟

模型采用美国AFF 模型（图4.31）， AFF 模型由拱形头部、 圆柱弹身和四片“十”字形尾翼组成。 弹长为457.2 mm， 弹径为45.7 mm， 弹体长径比L/D ＝10， 尾翼净半展长为22.8 mm。 参考长度为弹径， 参考面积为弹底面积， 力矩参考点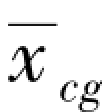 ＝0.5。

图4.31　基本模型AFF 外形图

如图4.32 所示， 计算网格均采用了贴体网格， 网格总量约为500 万。 取壁面第一层网格高度为5 ×10 －6m， 使得无量纲距离y ＋≤1。 同时， 保证壁面附近15 层网格的增长率为1.1。 扰动在亚声速流场中会传遍各处， 计算域长度为10 倍弹长， 宽度为50 倍弹径， 边界条件为压力远场条件。 扰动在超声速流场中的传播仅限于马赫锥内， 所以头部和周向边界条件为压力远场条件， 弹底网格边界条件为压力出口条件。

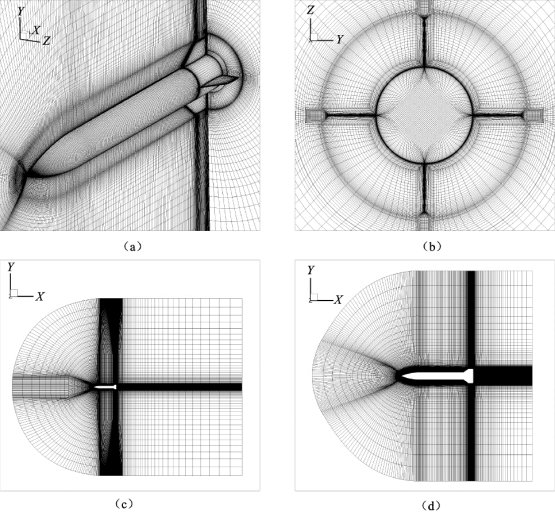
图4.32　AFF 模型计算网格示意图

（a） 弹体附近网格； （b） 弹底网格； （c） 亚声速计算域； （d） 超声速计算域(www.xing528.com)

图4.33 给出了不同湍流模型计算得到的AFF 外形马格努斯力系数和马格努斯力矩系数均值并与试验结果进行对比。 CFD 计算的马赫数Ma∞＝2.5， 无量纲转速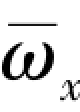 ＝0.025， 雷诺数Red ＝2.57 ×105。 试验结果为1976 年美国阿诺德空军基地工程研发中心的风洞试验数据[11]。 由图4.33 可知， 使用Transition 湍流模型得到的结果在α ＝12.0°和α ＝20.0°时与试验值最为接近， 介于试验值和其他湍流模型的结果之间， 同时马格努斯力系数和马格努斯力矩系数随攻角的变化趋势与试验吻合较好。 由图4.33 （a） 可知， 除Transition 模型外， 其他湍流模型在α ＝12.0°计算结果均为负值， 与试验值反向。 此外， 由数值模拟得到的尾翼－弹身组合体马格努斯力系数均值为正， 与单独弹身的马格努斯力系数方向相反。

图4.33　马格努斯力系数和马格努斯力矩系数随攻角的变化曲线

图4.34 所示为AFF 外形在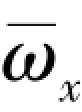＝0.025 时， 不同攻角下马格努斯力和力矩系数随马赫数的变化曲线。 由亚声速向超声速变化时， 马格努斯力和力矩系数会发生换向， 就绝对值而言是先增后降。 跨声速时尾翼－弹身组合体的马格努斯力和力矩系数变化较为剧烈。 进入超声速后， 随着马赫数增大， 马格努斯力和力矩系数量值逐渐减小。 在超声速时， 数值计算得到的马格努斯力和力矩系数与试验值吻合较好， 误差明显要小于亚声速的值。

图4.34　AFF 组合体马格努斯力和力矩系数随马赫数的变化曲线

（a） 马格努斯力系数； （b） 马格努斯力矩系数