边界层非对称转捩对弹箭旋转效应的影响

旋转弹身更为重要的流动现象， 发生在边界层从层流向湍流转捩的过程中。Sturek[8]使用热线试验和火花摄像观测了超声速小攻角下绕圆锥的流动， 并且发现旋转使锥体的转捩位置沿着旋转方向发生偏离。 图4.19 给出的不旋转时圆锥的转捩位置基本对称于攻角平面， 即圆锥两侧的层流区和湍流区的范围是相当的。 当圆锥旋转后， 转捩位置不再对称于攻角平面， 即圆锥两侧的层流区与湍流区范围不再相等。 由于转捩区内压力和摩擦力分布的畸变， 会在圆锥上诱导马格努斯力。

图4.19　转速引起的转捩线偏转

（α ＝4°， Ma∞＝2.0， ωx ＝333 r/s， Rel ＝5.9 ×106）

为了研究旋转弹身的非对称转捩过程中层流与湍流边界层的特性以分析得到非对称转捩对马格努斯力的影响， 采用了γ 转捩模型和添加转捩线的方法对旋转圆锥的流场进行模拟[9]。 采用双时间步法求解非定常N－S 方程， 刚性动网格技术模拟旋转。

圆锥模型及坐标系如图4.20 所示， 其中半锥角θc ＝10°， 锥总长L ＝220.47 mm，底部直径D ＝77.79 mm。 为了正确捕捉边界层的层流、 湍流和转捩现象， 要求选用的计算网格的法向网格增长率应该在1.1 ~1.2， 物面上沿流动方向至少布置100 个节点， 并且所用计算模型第一层网格的y ＋<1。 计算网格示意图如图4.21 所示， 计算条件为Ma∞＝2.0， ωx ＝333 r/s， 攻角α 为4°、 6°和8°和攻角α 为－4°和－6°时， 雷诺数Rel ＝6.1 ×106， 而α ＝±2°， 对应的雷诺数Rel ＝5.9 ×106。

图4.20　圆锥模型及坐标系示意图

图4.22 给出了三种模拟方法得到的结果与试验结果的对比。 由图可以看出， γ －Reθt转捩模型计算得到的转捩线， 虽然沿着旋转方向有偏移， 但是量很少， 而且转捩位置与试验结果相差较大。 在γ 转捩模型中， 层流边界层区域随着圆锥旋转方向发生偏转， 与试验结果还是有一定的差距。 通过合理设定转捩线位置所得的转捩结果与试验值符合得较好， 转捩位置比试验结果稍有延迟。 层流边界层随旋转方向发生明显的偏转。

图4.21　圆锥的计算网格

（a） 头部网格； （b） 整体网格

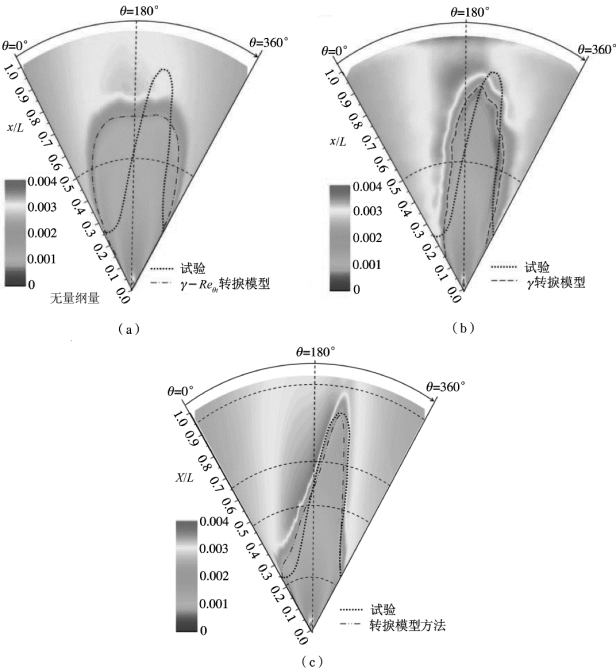
图4.22　旋转圆锥表面摩阻分布

（a） γ－Reθt转捩模型； （b） γ 转捩模型； （c） 转捩线方法
（α ＝4°， Ma∞＝2.0， ωx ＝333 r/s， Rel ＝6.1 ×106）(www.xing528.com)

表4.1 给出了γ－Reθt转捩模型、 γ 转捩模型以及转捩线方法计算得到的压力差引起的马格努斯力系数Cz－p以及摩擦力引起的马格努斯力系数Cz－τ与试验结果的对比。 由表可以看出， 转捩线方法与试验的转捩位置一致， 因此马格努斯力也与试验的吻合最好，γ 转捩模型虽然转捩位置不完全与试验结果一致， 但是成功地预测了转捩位置偏转， 得到的Cz－τ也与转捩线方法得到的值在量级上一致。 而γ －Reθt转捩模型预测的值与转捩线模型以及试验值相差较大。 因此， γ 转捩模型可以较好地模拟旋转引起的转捩位置畸变。

表4.1　不同转捩模型得到马格努斯力对比（α ＝4°， Ma∞＝2.0， ωx ＝333 r/s， Rel ＝6.1 ×106）

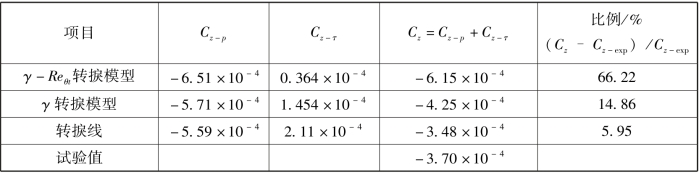
图4.23 为γ 转捩模型、 层流模型与湍流模型在ωx ＝333 r/s， x/L ＝0.50 处的摩擦阻力系数（简称摩阻系数） 与压力系数的分布图。 由图可以看出， ωx ＝333 r/s 时， 旋转圆锥绕流在x/L ＝0.50 横截面上， 在周向角θ ＝－50°与φ ＝100°附近边界层发生了转捩（定义边界层由层流完全转捩为湍流时为转捩位置）。 边界层由层流发展为湍流时，圆锥表面摩擦阻力系数出现了400%左右的增加。 由摩阻系数的周向分布图也可以看出， 圆锥两侧的转捩位置随着旋转方向偏转了50°左右。 由压力系数分布图来看， 由于圆锥中段的半径不大， 该处物面的周向速度较小， 旋转效应和边界层的非对称转捩并没有影响压力系数的峰值分布， 即压力系数的最大值和最小值分别位于θ ＝180°和φ ＝0°处。 对比θ ＝－50°与θ ＝100°的转捩位置可以发现， 在圆锥的两侧转捩位置的压力系数比层流与湍流结果出现了波动。 从压力系数在转捩位置附近放大图可以看出， 边界层转捩后， 转捩模型压力相比层流模型有明显的增大。 因此， 除旋转本身引起的摩阻系数与压力的畸变外， 由于由边界层非对称转捩所引起摩擦力的非对称分布和压力系数的非对称分布都会对面外力和力矩有贡献。

图4.24 所示为不同转速下， 由γ 转捩模型计算所得的x/L ＝0.50 处的边界层厚度分布与摩阻系数对比图。 由摩阻系数突变位置可以看出在此截面上的转捩位置。 对比两图可以发现， 边界层突然增厚位置与边界层转捩位置相对应， 即边界层由层流转捩为湍流时， 使边界层也突然增厚。 因此， 转速圆锥的边界层非对称转捩也会引起边界层厚度的非对称畸变。 当转速为零时， 边界层为对称分布， 且θ ＝0°位置为边界层最大厚度位置。 当转速不为零时， 由于此处半径较小， 最大厚度边界层位置向旋转的偏转不明显。但是， 随着转速的增大， 边界层的非对称性随着转速的增大更加明显。 边界层最大厚度位置沿着转速方向偏转， 转速越大， 偏转程度越大。

图4.23　表面摩阻系数和压力系数

（ωx ＝333 r/s， x/L ＝0.50）

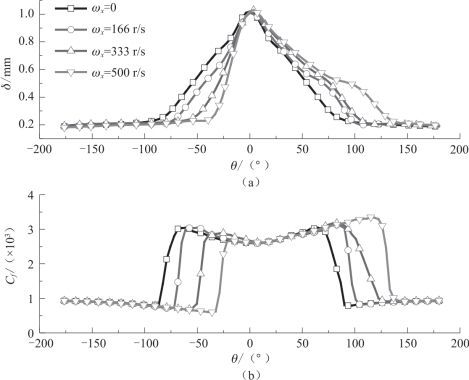
图4.24　边界层厚度δ 以及表面摩阻Cf （x/L ＝0.50）

由边界层厚度的分布曲线可以看出， 不同转速的边界层最大厚度都位于θ ＝0°附近， 旋转速度并没有使边界层的最大位移厚度发生偏移。 边界层由层流向湍流转捩后，边界层厚度会突然增加。 由于旋转使得转捩位置向右侧偏移， 转速越大， 偏移量也越多。 因此， θ ＝0°左侧区域边界层厚度变薄； θ ＝0°右侧边界层厚度在转捩区域变厚。 也就是说， 旋转会加剧由于转捩而引起的边界层位移厚度的畸变。 由摩阻系数Cf分布曲线也可以看出， 不同转速下摩阻系数Cf沿周向的分布还依然保持由层流摩阻系数和湍流摩阻系数组成的模式。 只是随着转速增大， 边界层转捩的位置沿着旋转方向偏移， 摩阻系数Cf由层流值与湍流值转换的位置向右偏移。 摩阻系数Cf的非对称分布将会加大黏性力对马格努斯力的贡献。

图4.25 所示为不同转速下的ΔCp0随θ 的变化。 对比边界层厚度的分布可以看出， 由于θ ＝0°左侧区域边界层厚度变薄， 因此该区域的压力系数突然减小。 特别是在θ ＝－75°转捩区域附近， ΔCp0 （θ） 的量值突然减小了90% （ωx ＝333 r/s 时， γ转捩模型与全层流模型对应的值相比）。 在θ ＝75°转捩区域附近， ΔCp0 （θ） 的量值突然增大了92% （ωx ＝333 r/s时， γ 转捩模型与全层流模型对应的值相比）。 由此可知， 边界层的非对称转捩会引起边界层位移厚度的非对称畸变， 使得横截面上压力的非对称分布， 产生马格努斯力。

图4.25　ΔCp0随周向角θ 的变化曲线