边界层非对称分离：弹箭旋转的空气动力效应

在如图4.13 所示的大攻角下， 弹身绕流出现分离， 在弹身的背分面形成一对分离涡。 当攻角不太大时， 背风区的一对分离涡对称于攻角平面。 但随着弹身的旋转， 分离涡向旋转方向偏转。 左侧的涡受到抑制， 向弹身靠近； 而右侧涡的分离点则向旋转方向偏转， 并且强度增加。 即在攻角不大时， 旋转诱导了弹身的非对称分离， 进而产生了马格努斯力。 为了研究较大攻角下， 弹体分离涡对旋转空气动力效应的影响， 采用双时间步法求解了非定常N－S 方程， 计算了大长径比“阿帕奇” （Apache） 弹身模型的旋转绕流场， 弹身的旋转运动采用刚性运动网格技术实现。

图4.13　旋转引起的边界层非对称分离[6]（攻角α ＝20°， V∞＝18.3 m/s， 顺时针旋转）

（a） 转速为零； （b） 中等转速； （c） 高转速

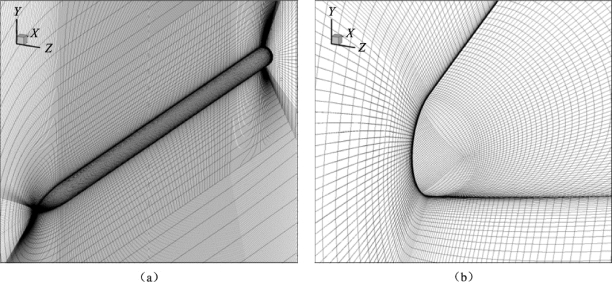
图4.14　Apache 弹身附近计算网格示意图

图4.15 给出了来流雷诺数ReD ＝1.54 ×107， 转速＝0.011 时， Apache 弹身的马格努斯力系数随攻角变化曲线的CFD 计算结果与试验结果[7]的比较。 可以看出， 马赫数Ma∞＝3.0 的CFD 数值模拟结果与试验值的吻合较好。 而且大长径比弹身马格努斯力系数随攻角非线性变化较为明显。 当马格努斯力特性进入非线性区后， 马格努斯力随攻角的增大而减小， 在攻角不太大时就有换向的趋势。

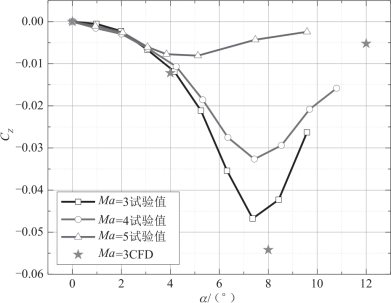
图4.15　Apache 弹身马格努斯力系数随攻角的变化曲线

(www.xing528.com)

图4.16　Apache 弹身表面压力和横截面流线图

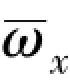（＝0.011， ReD ＝1.54 ×107， Ma∞＝3.0， α ＝4°）

为了分析大长径比弹身马格努斯力换向的原因， 给出了弹身不同攻角时不同横截面位置处的压力云图、 流线图和弹身背风面分离体涡图（图4.16）。 由图可以看出， 由于弹身长径比大， 在α ＝4°， 就出现了体涡非对称分离， 弹体的分离涡在小攻角下就大范围地占据弹身后体区域， 大大加强了体涡在弹身马格努斯力中的比重。 弹身分离涡的影响直接体现在了弹身横截面上的压力分布[图4.17 （a）]， 虽然出现了体涡的非对称分离， 但是几个弹身几个截面上的压力系数ΔCpz ＝ [Cp·nz]right － [Cp·nz]lift分布基本上还是随着弹身向后而出现线性增大， 其作用与边界层位移厚度所表现出来的效果一致。 攻角增大到12°时， 弹身体涡分离使得x/L ＝0.91 截面上的压力差由负值变为正值[图4.17 （c）]。

图4.18 所示为法向力系数和马格努斯力系数沿弹身轴线的分布曲线。 由图可以看出， 法向力系数在头部迅速增大， 之后逐渐降低并趋于平缓。 法向力系数随攻角的增大近似于线性增大。 马格努斯力系数沿弹身的分布较为复杂， 攻角不大时与小长径比弹身的马格努斯力分布近似， 并且随攻角的增大而线性增大。 当攻角增大到12°后， 弹身后体的马格努斯力系数出现了换向， 并且越向后系数的量值线性越大。

图4.17　Apache 弹身截面的ΔCpz 曲线（Ma∞＝3.0）

（a） α ＝4°； （b） α ＝8°； （c） α ＝12°

图4.18　气动力系数沿弹轴的分布曲线

（a） 法向力系数； （b） 马格努斯力系数