弹箭空气动力-边界层厚度非对称偏移

弹身旋转运动使得边界层向旋转方向偏转， 弹身旋转转进侧的边界层位移厚度将大于旋转转出侧， 如将边界层位移厚度等效为旋转弹身在无黏流中的实际外形， 可以看出转进侧的压力会大于转出侧的压力， 进而诱导产生指向转出侧的马格努斯力（图4.5）。但是， 由于旋转引起的两侧周向速度不对称同时也将导致径向压力梯度不对称， 也会诱导马格努斯力。

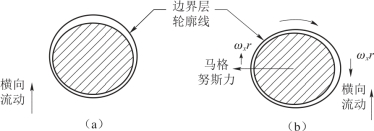
图4.5　旋转引起的边界层畸变

（a） ωx ＝0； （b） ωx >0

4.2.1.1　基于移动壁面法的数值模拟

单独弹身旋转引起的边界层位移厚度畸变可以采用基于壁面速度的方法进行模拟。图4.6 给出了SOCBT 外形采用数值方法得到的由压力差引起的马格努斯力分量与由摩擦切应力引起的马格努斯力分量沿弹轴的分布以及与试验结果的比较[4]。 试验中为了得到湍流边界层， 在弹头部40.6 英寸处设置了宽度为4.6 英寸的强制转捩装置。 计算条件如图4.6 中所示， 马赫数Ma∞＝2.0， 攻角α ＝2°， 转速ωx ＝333 r/s， 雷诺数Re ＝2.11 ×107， 湍流模型为B－L 模型。 由马格努斯力系数的分布图可以看出， 压力差引起的马格努斯力与摩擦力引起的马格努斯力都沿弹轴向后逐渐增大， 在弹尾处量值最大。压力差引起的马格努斯力与摩擦引起的马格努斯力方向相反， 其中压力差引起马格努斯力在量值上占主导。

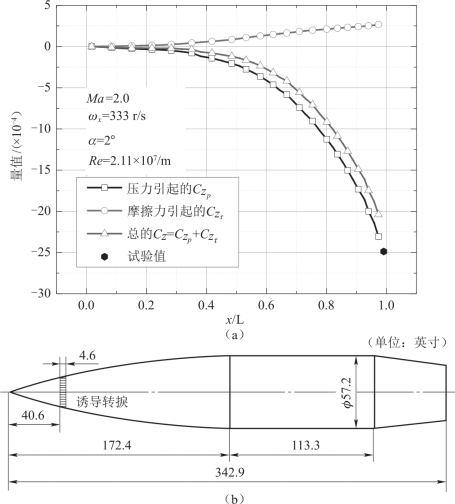
图4.6　SOCBT 外形马格努斯力的组成与分布

4.2.1.2　基于滑移网格技术的数值模拟

为了比较不同转速下边界层位移厚度与马格努斯力的分布变化， 采用双时间步法求解了非定常N－S 方程， 计算了SOC 弹身外形的旋转绕流场。 SOC 外形为拱形头部＋圆柱弹身， 弹身长度为6d， 头部长度为3d （d 为弹身的直径）。 计算条件为来流马赫数Ma∞＝3.0， 转速ωx ＝500 r/s， 雷诺数ReL ＝7.6×106。 SOC 采用了贴体网格， 弹身周向网格数为100， 法向网格数为80， 纵向网格数为100， 弹身上的y ＋<1， 法向网格增长率为1.1 ~1.2。 采用了γ－Reθt湍流模型。

计算中弹身的旋转采用了滑移网格技术实现。 如图4.7 所示， 计算域的内域网格包含弹身， 而外域网格在内域网格的外部。 计算时， 内域网格以设定的转速旋转， 外域网格不旋转。 在交接面上， 内外域网格并不是点对点的， 信息通过面插值进行传递。

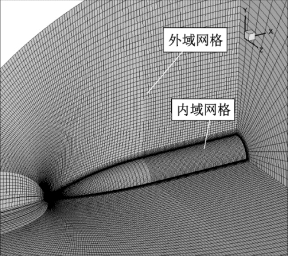
图4.7　SOC 模型与网格图

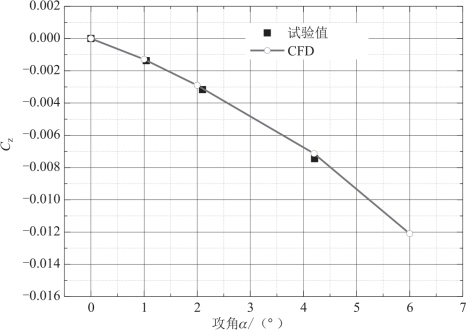
图4.8 所示为不同攻角下马格努斯力系数Cz的计算结果与试验值[5]比较。 由图可以看出小攻角下， 计算结果与试验结果很吻合， 两者偏差小于5%， 验证了计算方法的有效性。

(www.xing528.com)

图4.8　SOC 马格努斯力随攻角变化曲线

对比转速ωx ＝0 和ωx ＝500 r/s 弹身的极限流线以及各截面的涡量分布云图可以看出， 边界层的厚度顺着流动的方向逐渐增加， 弹身表面的极限流线也由于旋转而向旋转方向发生偏转（图4.9）。 在攻角α ＝4.2°时， 弹身压力分布和表面极限流线都会由于旋转而不再对称。 横截面的流动没有发生分离， 但是横截面两侧的边界层不再对称， 而是向旋转方向发生偏转（图4.10）。 由边界层的偏转引起的压力差产生马格努斯力， 而且转速越大， 边界层偏移的量也越大， 转速高的边界层厚度也明显大于转速低时的边界层厚度。

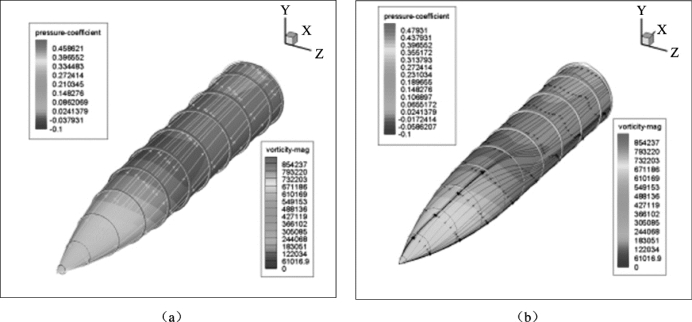
图4.9　弹身的极限流线、 压力系数与截面的涡量图（α ＝4.2°）

（a） ωx ＝0； （b） ωx ＝500 r/s

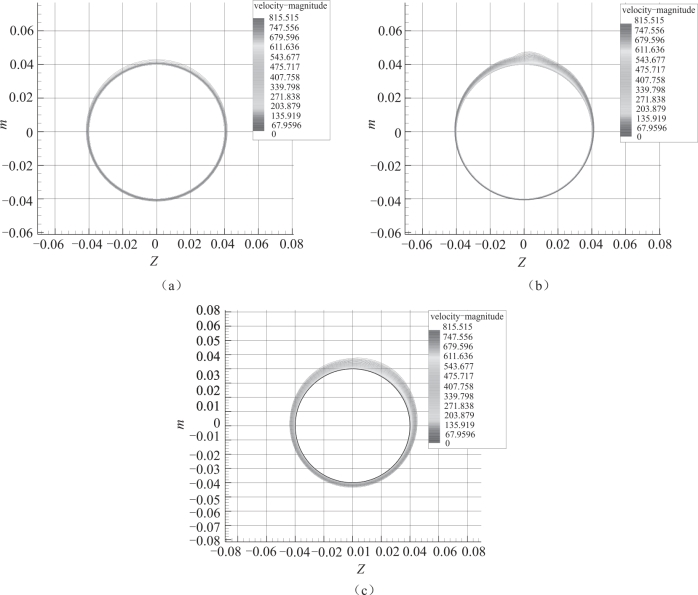
图4.10　横截面边界层位移厚度分布（α ＝4.2°， x/d ＝5.9）

（a） ωx ＝0； （b） ωx ＝333 r/s； （c） ωx ＝500 r/s

由SOC 外形的法向力系数和马格努斯力系数沿弹身分布曲线（图4.11） 可以看出， 马格努斯力系数与法向力系数沿弹身的分布不同， 弹身的法向力系数主要与弹身的横截面面积变化相关， 即在头部区域由于横截面面积的变化率为正， 因此法向力系数为正且相对较大。 而在后体区域， 弹身的横截面面积不变， 但是由于黏性作用， 法向力系数并没有立刻变为零， 而是沿轴向方向逐渐减小。 在小攻角下， 转速增大对法向力系数影响不明显。 马格努斯力系数沿弹身的分布与法向力的分布明显不同。 弹身后体的马格努斯力系数明显增大， 这与边界层的厚度沿弹身向后发展逐渐增大相关， 即由于边界层的畸变引起的压力差也逐渐增大， 马格努斯力系数也越大。

图4.12 所示为弹身x/d ＝5.9 截面处， 截面上的压力系数的分布曲线。 由压力系数分布可以看出， 旋转引起弹身两侧的压力不对称。 在攻角α ＝4.2°时， 旋转使得压力系数的绝对值在周向角θ ＝90°附近减小， 在周向角θ ＝270°附近增大， 而且随着转速增大压力系数的变化量也增大。

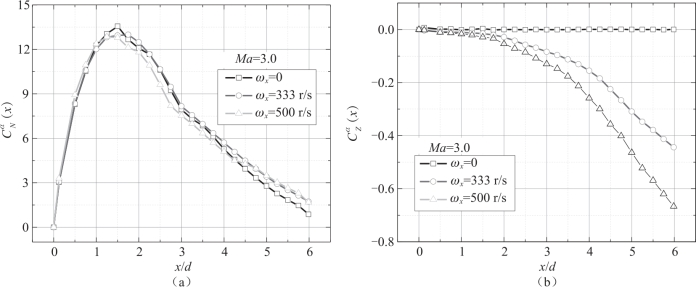
图4.11　SOC 外形气动力系数沿弹身分布

（a） 法向力系数导数； （b） 马格努斯力系数导数

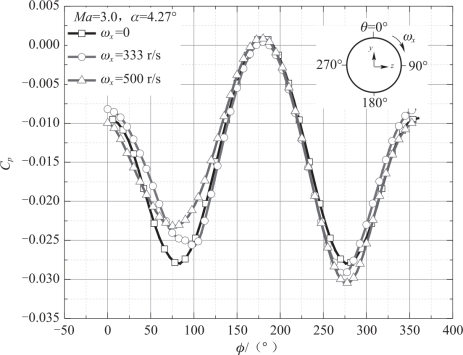
图4.12　弹身截面处压力系数沿周向角的分布（x/d ＝5.9）