【摘要】：谐波平衡法相对于双时间推进法最主要的特点是不需要进行物理时间推进， 将非定常问题完全转化为了定常问题。因此， 采用谐波平衡法进行模拟时， 在一定条件下比采用双时间推进法更高效。旋转尾翼－弹身组合体绕流场明显是周期性的， 因此可以使用谐波平衡法模拟旋转弹箭的绕流场[2]。由式 可以得到离散时刻的时间导数：用式 取代式（4.3） 中的时间导数项， 则非定常方程变换为定常方程， 可以使用定常的方法求解。
谐波平衡法相对于双时间推进法最主要的特点是不需要进行物理时间推进， 将非定常问题完全转化为了定常问题。 因此， 采用谐波平衡法进行模拟时， 在一定条件下比采用双时间推进法更高效。 旋转尾翼－弹身组合体绕流场明显是周期性的， 因此可以使用谐波平衡法模拟旋转弹箭的绕流场[2]。
在周期性流动问题中， 对于以任意的时间T 为周期的与时间相关的周期性变化物理量w（x， t）， 可以表示为m 阶的傅里叶级数：
式中， m 为谐波数； ω 为物理量变化频率； w（x， t）为空间位置x ＝（x， y， z）在t 时刻的物理量值； 2m ＋1 为将离散的傅里叶级数反变换回时域对应的离散时域时刻的数量， 也是未知的傅里叶系数的数量； 
（x）为x 处的时均值； 
为傅里叶系数。
由式（4.17） 可以得到离散时刻的时间导数：(www.xing528.com)
用式（4.19） 取代式（4.3） 中的时间导数项， 则非定常方程变换为定常方程， 可以使用定常的方法求解。 当计算收敛时， 便可得到在N 个时域时刻流场的全部物理量，而周期中其他时刻的物理量则可以根据系数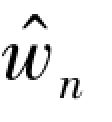
的插值得到。
对于旋转翼身组合体的绕流场， 需要采用计算域旋转的方式定义弹箭的运动。 定义计算域绕x 轴旋转， 则计算域中任意初始时刻坐标为（x0， y0， z0） 的空间点在物理时间为tk 的第k 个离散时刻的y、 z 坐标ytk、 ztk分别为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
