弹箭旋转空气动力效应

早期弹身旋转空气动力效应通过分别求解边界层方程与外部无黏流动方程来实现【1】。

弹身的边界层方程为

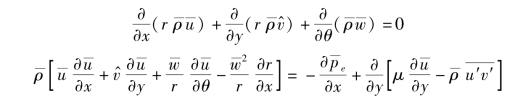
迭代求解的主要计算步骤如图4.1 所示。 给定马赫数、 攻角、 壁温、 转速， 以及来流特性， 计算得到弹身无黏流动方程的解u、 w、 T、 p 等。 以此为边界条件以及不旋转层流边界层的速度型为初始条件， 代入边界层流动方程（4.1） 和（4.2）， 计算得到边界层流动参数， 包括壁面切应力和径向压力梯度对旋转空气动力效应的贡献以及纵向和周向的边界层位移厚度分布。 通过纵向和周向边界层位移厚度， 计算得到弹身的三维边界层位移厚度。 将三维边界层位移厚度叠加到弹身上， 得到虚拟弹身外形， 此时的弹身外形包含了边界层位移厚度的非对称分布。 再对虚拟弹身外形进行无黏流的计算， 得到边界层位移厚度畸变引起的马格努斯力和力矩。 综合边界层计算中得到的纵向切应力、周向切应力和径向压力梯度对马格努斯力和力矩的贡献， 边界层位移厚度对马格努斯力和力矩的贡献、 得到总的马格努斯力和力矩。(www.xing528.com)

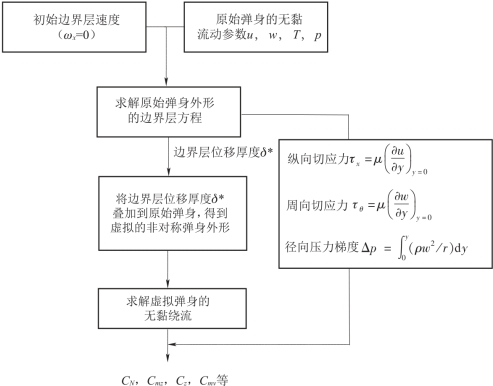
图4.1　边界层方程与无黏流动方程的迭代求解过程

图4.2 所示为在Ma∞＝3.0、 ＝0.283 时， 用边界层方法与外部无黏流迭代计算得到SOC 弹身的马格努斯力系数与试验结果进行比较。 图中Cz－τx、 Cz－τθ和Cz－Δp分别为纵向切应力、 周向切应力和径向压力梯度对马格努斯力的贡献； Cz－BL为边界层内三个量的贡献总和， 即Cz－BL ＝Cz－Δp ＋Cz－τθ ＋Cz－τx； Cz－BL ＋δ∗为边界层内三个量和边界层位移厚度对马格努斯力贡献的总和， 即弹身总的马格努斯力系数。 由图4.2 可以看出， 计算得到的总马格努斯力系数与试验值吻合较好。 在各种马格努斯力的分量中， 边界层位移厚度畸变的贡献最大， 纵向切应力对马格努斯力的贡献很小， 周向切应力对马格努斯力的贡献与边界层位移厚度和径向压力梯度的贡献方向相反。

图4.2　SOC 弹身外形由迭代方法计算得到Cz 与试验值的比较【1】