弹箭旋转对层流边界层的影响

2.3.1.1　边界层方程

在图2.4 所示的柱坐标系中， 定常N－S 方程为

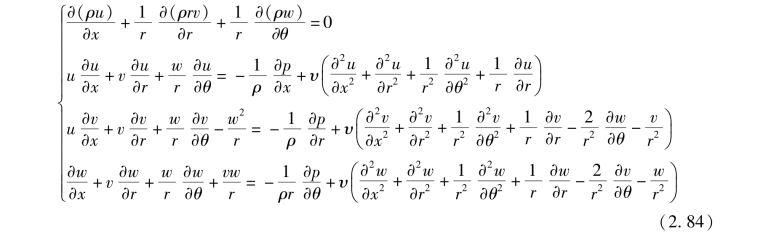
对于θ 向的动量方程主要确定周向速度分布， 而理论研究已经找到与实际符合的周向速度表达式， 这里不再考虑该方程。 在边界层内假设密度不变， 可以简化连续方程。对x 向和r 向动量方程中的各项进行量级分析， 略去高阶项， 得到简化的边界层方程为

边界层位移厚度为

边界层厚度为

2.3.1.2　边界层的Mangler 变换

在零攻角时旋转体上的可压缩层流边界层， 可以采用式（2.86） 进行Mangler 变换得到。 Mangler 变换式为

假设边界层外缘速度等于自由流速度， 即uδ ＝V∞， 密度和黏度可以作为平均值或有效值处理， 则式（2.88） 和式（2.89） 可写为

式中， “ －” 表示取平均值； ro 为弹身的当地半径。

式中， 第一个因子是平板不可压缩布拉休斯层流边界层的解； 第二个因子是压缩性修正； 第三个因子是外形Mangler 变换的稍微修改形式， 压缩性修正为

式中， 层流恢复系数γ ＝0.85； 湍流恢复系数γ ＝0.896。

对于在连续运行风洞中的气流， 可以进一步简化压缩性修正， 因为在风洞温度范围内黏度指数λ ＝1.00， 并且壁温Tw 等于绝热近似壁温Taw， 则

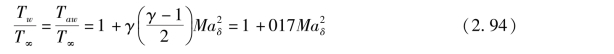
在风洞试验中， 有

对于尖头细长体可以假设边界层外缘马赫数Maδ 等于自由流马赫数Ma∞。 在飞行的情况下， 应使用和实际壁温与飞行边界层温度一致的λ。 由式（2.95） 和式（2.92）得到

式中， k 为压缩性修正系数； mn 为弹箭头部的Mangler 变换系数； mα，ωx为考虑到攻角和旋转的Mangler 变换系数。

如果尖拱形头部的母线方程为则弹箭头部的Mangler 变换系数可以表示为

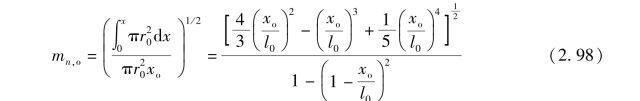
式（2.98） 的线性近似解为

式中， 下标“o” 表示ogive， xo 为拱形头部坐标； l0 为拱形头部长度； ra 为拱形头部最大半径。

图2.7　尖拱形头部的　Mangler 变换系数

式（2.100） 中几何变换系数的定义如图2.8 所示。

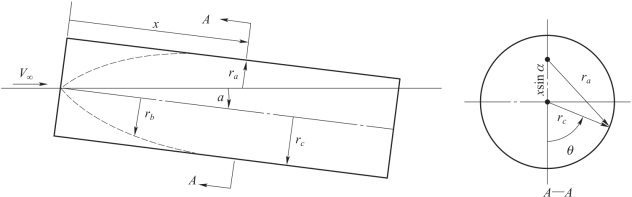
图2.8　攻角变换系数几何参数

这样可以得到有效周向角为

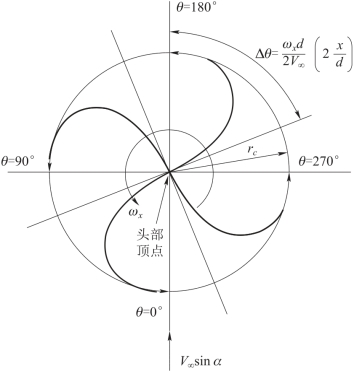
图2.9　旋转弹身边界层内的流线分布

将式（2.100） 中的周向角θ 替换为考虑了旋转效应的有效周向角ϑ [式（2.102）]，

得到mα，ωx的表达式为

式（2.103） 就是完整的攻角与转速的Mangler 变换式。 得到Mangler 变换式后的边界层厚度参数为

2.3.1.3　周向速度型

在小攻角下， 半径r0 的弹身以转速ωx 旋转， 如果边界层流动没有出现分离， 依然附着在物体表面。 此时假设边界层流动依然为层流状态， 则弹身横截面上边界层内的周向速度分布可以表示为

(www.xing528.com)

由式（2.105） 和式（2.106） 可以给出弹身横截面内的周向速度分布。 当f′ ＝0时， 弹体表面仅剩下由旋转引起的周向速度rbωx； 当f′＝1 时， 仅剩下横向流动所决定的无黏流速度2V∞sinαsinθ， 这与边界层内流动的边界条件符合。 值得注意的是， 此时，2V∞sinαsinθ 项是从势流理论中得到的， 没有考虑体涡的影响。 因此， 该模型仅适用于小攻角情况。 当攻角增大后， 需要考虑在圆柱后体上形成体涡的影响， 需要对2V∞sinαsinθ 进行修正。

2.3.1.4　边界层位移厚度的贡献

当存在攻角和转速时， 弹身截面左、 右两侧边界层位移厚度差可由对不可压缩层流边界层的布拉修斯解进行压缩性修正后给出：

其中，

式中， Maδ 为边界层外缘的马赫数， 对于长径比较大的弹体通常可以取为来流马赫数Ma∞。

将式（2. 108）、 式（2.109） 和式（2.110） 代入式（2.107）， 并简化得到

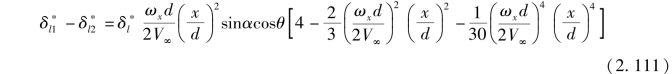
按照细长体理论， 由边界层位移厚度引起的弹体横截面两侧的压力差可表示为

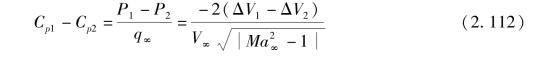
弹体两侧的扰动速度可以表示为

式中， Φ∗＝ux－vrs 为边界层位移厚度上的扰动速度势， 可以表示为

将当地边界层位移厚度等效为物体壁面后， 径向速度差可以表示为

联立式（2. 111） ~式（2. 115）， 可以计算边界层位移厚度畸变诱导的压力差为

2.3.1.5　径向压力梯度的贡献

径向压力梯度对马格努斯力的贡献可以通过边界层模型N －S 方程的径向压力梯度和连续性方程得到。 将周向速度分布式（4.1） 和式（4.2） 代入不可压缩连续性方程， 有

沿r 积分后可以得到不可压缩流的弹身径向速度， 以T′/T∞体现气流的压缩性修正效应， 可以得到径向速度的表达式

将式（2.120） 化简积分后， 得到

由旋转导致的弹身边界层非对称分布诱导的马格努斯力中， 由压力引起的项主要包括边界层位移厚度畸变所引起的压力差[式（2.116）]； 以及由径向压力梯度所诱导的压力差[如式（2.121） ~式（2.123）]。 得到总压力差对马格努斯力的贡献为

其中，

当忽略的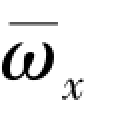非线性项时， Hl 是马赫数的函数， 称为马格努斯力压缩性因子。 马格努斯力与马赫数的关系由Hl 体现。 风洞试验与飞行试验都表明， 在跨声速时， 马格努斯力会突然增大。 对于尾翼稳定的旋转弹来说， 要特别关注跨声速时的动稳定性。

2.3.1.6　体涡影响的修正

式（2.123） 中的2V∞sinαsinθ 是按位流理论确定的周向速度。 在黏性流动中， 它就是边界层外缘处的周向速度。 周向速度分布模型， 仅能表示有攻角时拱形头部的表面速度， 而由于后体上生成的体涡， 需要对速度分布进行修正。 根据油流试验整理得到的后体上无黏周向速度为

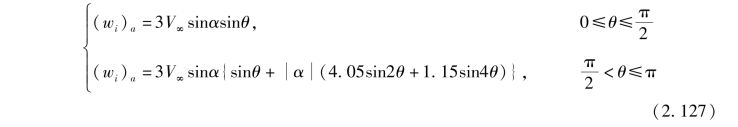
这样对于弹身头部的马格努斯力可以采用式（2.124） 进行计算， 而后体用式（2.127） 替换式（2.124） 中的2V∞sinαsinθ 项， 计算后体的压力差为

弹身后体的侧向压力差为

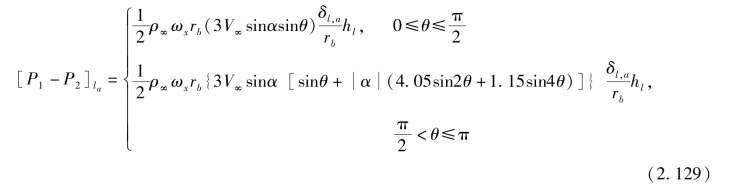
2.3.1.7　马格努斯力和力矩系数

将侧向压力差公式（2.129） 沿弹身纵向和周向进行积分， 得到马格努斯力

式中， ln 为头部长度； l 为全弹长度。

将式（2.128） 和式（2.129） 代入式（2.130）， 得到

马格努斯力系数导数为

马格努斯力矩系数导数为

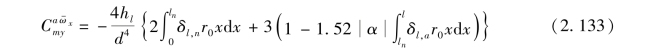
对弹身的积分需要根据弹形和边界层厚度才能完成。