对保险中介行业宏观层面上的效率评估,层次分析法(Analytic Hierarchy Process,AHP)是最适合的。层次分析法是20世纪70年代中期由美国著名运筹学家萨蒂(Saaty)提出的。这是一种依据序标度,将系统因素按支配关系分组以形成有序的递阶层次结构,通过两两比较判断方式以确定每一层次中因素的相对重要性;然后在递阶层次结构内进行合成,以得到决策因素相对于目标的重要性总顺序,从而为决策提供确定性判据的方法。AHP本质上是一种决策思维方法,整个过程体现了人的决策思维的基本特征,即分解、判断与综合,便于决策者之间彼此沟通,是一种十分有效的系统分析方法。它既采用具有适应环境变化的灵活性的“相对标度”,同时又充分利用了专家的经验和判断,并能对其误差作出估计。在层次分析法中,比例标度采用1~9之间的整数及其倒数。用比例标度测量的结果表示为正反判断矩阵,因而这个矩阵也可以看作是这组元素在此属性下的测度。
保险中介公司管理人员需要对公司未来最有效发展路径进行决策,可选择的方案是增开各地的分公司,加大公司业务的广度或重点培养原有几个城市的业务发展,增加业务的深度。除了考虑经济效益外,还要考虑公司成本、人力成本等因素,是多准则决策问题,考虑运用层次分析法解决。采用层次分析法对保险中介行业效率进行评估的步骤可以叙述如下:
1. 建立递阶层次结构
应用AHP解决实际问题,首先要明确分析决策的问题,并把它条理化、层次化,理出递阶层次结构。AHP要求的递阶层次结构一般由以下三个层次组成:一是目标层(最高层),指问题的预定目标;二是准则层(中间层),指影响目标实现的准则;三是措施层(最低层),指促使目标实现的措施。
通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是明确的。最后分析解决问题(实现决策目标),在上述准则下,有哪些最终解决方案(措施),并将它们作为措施层因素,放在递阶层次结构的最下面(最低层)。明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构成了递阶层次结构。
那么,在上面保险中介公司的决策过程中,首先要建立递阶层次结构,在中介公司决策问题中,公司管理人员希望通过选择不同的发展方式,使综合效益最高,即决策目标是“公司未来如何发展使得公司效率最高”。为了实现这一目标,需要考虑的主要准则有三个,即经济效益、公司成本和业务发展难度。但问题绝不这么简单。通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便总公司管理、业务如何开展、公司人员如何培训等(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确,为了实现决策目标,在上述准则下可以有哪些方案。根据题中所述,本问题有两个解决方案,即大力发展分公司和加强原有公司的业务经营,这两个因素作为措施层元素放在递阶层次结构的最下层。很明显,这两个方案和所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。同时,为了方便后面的定量表示,一般从上到下用A,B,C,D,…代表不同层次,同一层次从左到右用1,2,3,4,…代表不同因素。这样构成的递阶层次结构如图3-2所示。
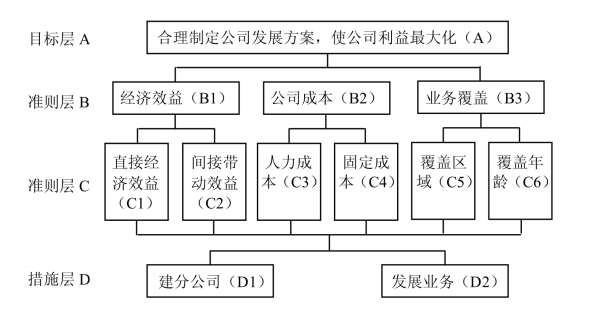
图3-2 递阶层次结构示意图
2. 构造判断矩阵并赋值
根据递阶层次结构就能很容易地构造判断矩阵。构造判断矩阵的方法是:每一个具有向下隶属关系的元素(被称作准则)作为判断矩阵的第一个元素(位于左上角),隶属于它的各个元素依次排列在其后的第一行和第一列。
重要的是填写判断矩阵。填写判断矩阵时,通常采取的方法是向填写人(专家)反复询问。针对判断矩阵的准则,将其中两个元素两两比较,看哪个重要,重要多少,对重要性程度按1~9赋值(重要性标度值见表3-3)。
表3-3 重要性标度值

设填写后的判断矩阵为![]() 判断矩阵具有如下性质:
判断矩阵具有如下性质:
(1)aij>0;(2)aji=1/ aji;(3)aii=1
根据上面性质,判断矩阵具有对称性,因此在填写时,通常先填写aii=1部分,然后仅需判断及填写上三角形或下三角形的n(n-1)/2个元素就可以了。在特殊情况下,判断矩阵可以具有传递性,即满足等式:
![]()
当上式对判断矩阵所有元素都成立时,则称该判断矩阵为一致性矩阵。
征求专家意见后填写好的判断矩阵如图3-3所示。
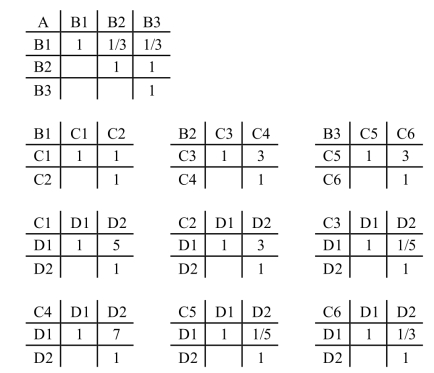
图3-3 判断矩阵
3. 层次单排序(计算权向量)与检验
对征求专家意见后填写好的判断矩阵,利用一定数学方法进行层次排序。层次单排序是指每一个判断矩阵各因素针对其准则的相对权重,所以本质上是计算权向量。计算权向量有特征根法、和法、根法、幂法等,这里采用的是和法。
和法的原理是,对于一致性判断矩阵,每一列归一化后就是相应的权重。对于非一致性判断矩阵,每一列归一化后近似其相应的权重,在对这n个列向量求取算术平均值作为最后的权重。具体的公式是:
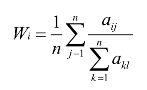
需要注意的是,在层次排序中,要对判断矩阵进行一致性检验。在特殊情况下,判断矩阵可以具有传递性和一致性。一般情况下,并不要求判断矩阵严格满足这一性质。但从数学规律来看,一个正确的判断矩阵的重要性排序是有一定逻辑规律的,例如,若A比B重要,B又比C重要,则从逻辑上讲,A应该比C明显重要。若两两比较时出现C比A重要的结果,则该判断矩阵违反了一致性准则,在逻辑上是不合理的。
因此在实际中要求判断矩阵满足大体上的一致性,需进行一致性检验。只有通过检验,才能说明判断矩阵在逻辑上是合理的,才能继续对结果进行分析。
一致性检验的步骤如下:(https://www.xing528.com)
第一步,计算一致性指标C.I.(consistency index):
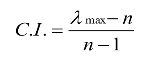
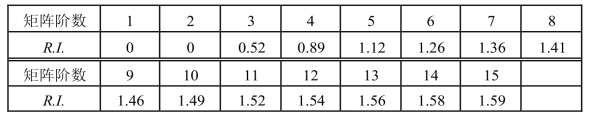
第二步,查表确定相应的平均随机一致性指标R.I.(random index)。
据判断矩阵不同阶数查表3-4,得到平均随机一致性指标R.I.。例如,对于5阶的判断矩阵,查表得到R.I.=1.12。
表3-4 平均随机一致性指标R.I.表(1000次正互反矩阵计算结果)
第三步,计算一致性比例C.R.(consistency ratio)并进行判断
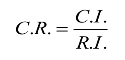
当C.R.<0.1时,认为判断矩阵的一致性是可以接受的;当C.R.>0.1时,认为判断矩阵不符合一致性要求,需要对该判断矩阵进行重新修正。
通过和法计算的权向量和检验结果如图3-4所示。
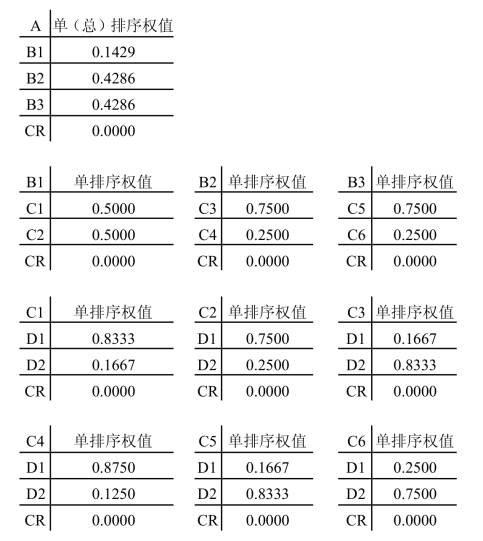
图3-4 层次计算权向量及检验结果
可以看出,所有单排序的C.R.<0.1,因此可以认为每个判断矩阵的一致性都是可以接受的。
4. 层次总排序与检验
总排序是指每一个判断矩阵各因素针对目标层(最上层)的相对权重。这一权重的计算采用从上而下的方法,逐层合成。很明显,第二层的单排序结果就是总排序结果。假定已经算出第k-1层m个元素相对于总目标的权重![]() 第k层n个元素对于上一层(第k层)第j个元素的单排序权重是
第k层n个元素对于上一层(第k层)第j个元素的单排序权重是![]() 其中不受j支配的元素的权重为零。令
其中不受j支配的元素的权重为零。令![]() 表示第k层元素对第k-1层元素的排序,则第k层元素对于总目标的总排序为:
表示第k层元素对第k-1层元素的排序,则第k层元素对于总目标的总排序为:
![]()
或
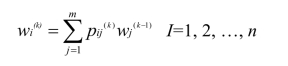
同样,也需要对总排序结果进行一致性检验。假定已经算出针对第k-1层第j个元素为准则的![]() 则第k层的综合检验指标为:
则第k层的综合检验指标为:
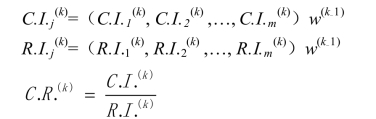
当![]() 时,认为判断矩阵的整体一致性是可以接受的。
时,认为判断矩阵的整体一致性是可以接受的。
上述的层次总排序及检验结果如表3-5所示。
表3-5 C层次总排序(C.R.=0.0000)和D层次总排序(C.R.=0.0000)
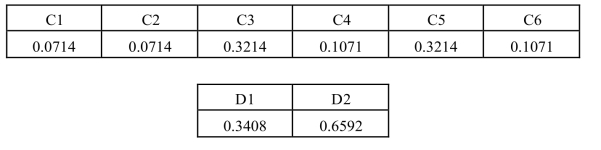
可以看出,总排序的C.R.<0.1,认为判断矩阵的整体一致性是可以接受的。
5. 结果分析
通过对排序结果的分析,得出最后的决策方案。从方案层总排序的结果看,发展原有优势业务(D2)的权重(0.6592)远远大于建立分公司(D1)的权重(0.3408),因此,最终的决策方案是发展原有优势业务。根据层次排序过程分析决策思路。对于准则层B的3个因子,直接经济效益(B1)的权重最低(0.1429),公司成本(B2)和业务覆盖程度(B3)的权重都比较高(皆为0.4286),说明在决策中比较看重公司成本和业务覆盖程度。对于不看重的经济效益,其影响的两个因子——直接经济效益(C1)、间接带动效益(C2)单排序权重都是建立分公司远远大于发展原有优势业务;对于比较看重的公司成本和业务覆盖程度,其影响的四个因子中有三个因子的单排序权重都是发展原有优势业务远远大于建立分公司。由此可以推导出,发展原有优势业务方案由于公司成本和业务覆盖程度较为突出,权重也会相对突出。从准则层C总排序结果也可以看出,人力成本(C3)、业务覆盖区域(C5)是权重值较大的,而如果单独考虑这两个因素,方案排序都是发展原有优势业务远远大于建立分公司。
由此我们可以分析出决策思路,即决策比较看重的是公司成本和业务覆盖程度,不太看重经济效益,因此对于具体因子,人力成本和业务覆盖区域成为主要考虑因素,对于这两个因素,都是发展原有优势业务方案更佳,由此,最终的方案选择发展原有优势业务也就顺理成章了。
在中介机构效率评估的宏观层面上,层次分析法可以很好地解决机构决策的有效性问题,但是各个中介机构都是由许多的分支机构组成的,而对于分支机构经营效率的评价,用层次分析法则不能很好地反映。这时因子分析法就能对所有琐碎的信息进行分类,从而更好地反映各个分支机构的效率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




