面板模型与保险中介从业人员数量的影响关系研究

上文通过翔实的数据描述了近些年来我国保险专业中介机构的发展，并且根据数据分析得出了目前保险专业中介发展的特点及趋势。但上述数据并未与保险市场的发展情况联系起来，因此在下面的实证分析中主要通过面板模型分析保险专业中介机构对保险市场的提升作用，特别是增加保险产品供给、扩大保险市场规模的作用。

1. 数据选择

为面板模型选择数据时，以全国各省份保险专业中介公司（包括保险专业代理机构与保险经纪机构，不包含保险公估机构）的机构数量、从业人员数量及营业收入作为面板模型的解释变量，以各省份的保费收入、保险深度及保险密度为被解释变量，分别建立面板模型。这里不包含保险公估机构的数据，主要是考虑保险公估机构的主要业务是核赔定损，并不是作为直接销售保险产品的中介机构，与本章建立面板模型想要证实的理论假设并不完全直接契合，因此被解释变量中并没有包括保险公估机构的数据。面板模型的时间序列跨度是从2004年至2010年，主要是考虑2003年及其之前《保险年鉴》中《各保险中介公司基本情况》中有很多省份的数据是空白，鉴于数据真实性要求以及保险专业中介机构也是近些年来才有了较快发展的考虑，笔者将面板数据的时间序列定为最近7年。

面板模型截面数据的样本包括安徽、北京、大连、福建、甘肃、广东、贵州、海南、河南、黑龙江、湖南、吉林、江苏、江西、辽宁、宁波、青岛、青海、厦门、山东、陕西、上海、四川、天津、新疆、云南、浙江、重庆，共28个省（直辖市、自治区、单列市）。原本数据包含了31个省份，外加5个单列市，共36个样本，但由于个别省份某一项数据缺失，笔者为保持原有数据的真实性而将其删掉，因此截面样本剩下28个省份。本章旨在通过几个不同的面板模型分别验证上文提到的理论假设1、2、3，并首先通过全国面板模型数据检验理论假设1，其次通过将28个省份样本分为发达保险专业中介机构地区及不发达保险专业中介机构地区来验证理论假设2和理论假设3。

2. 面板模型介绍

本章采用面板数据回归模型来研究保险专业中介机构对扩大保险市场的作用机制。面板数据模型的一般形式为：

式中，i=1， 2， …，N表示N个个体，在本章模型中即表示全部28个省份；t表示时间序列，即2004年至2010年；yit表示被解释变量对个体i在t时期的观测值，即28个省份在2004年至2010年的保费收入、保险深度与保险密度；xkit是第k个解释变量对于个体在t时的观测值，在本章模型中表示保险专业中介公司的机构数量、从业人员数量及营业收入规模；βkit是待估计的参数；uit是随机误差项。对面板模型作不同的限制假设，可以使其成为不同类型的面板数据模型。结合实际需要，本章的面板数据模型分为混合模型和不变系数（斜率）固定效应模型两种。

3. 全国面板模型

（1）以保费收入衡量保险市场下的混合面板

模型以上述28个省份的机构数量、从业人员数量、营业收入作为解释变量，以保费收入、保险深度及保险密度作为被解释变量，分别用JGSL、CYRY、YYSR、BFSR表示，其中机构数量的单位是个，从业人员数量的单位为位，营业收入的计量单位是百万元，为统一起见保费收入的计量单位也是百万元，保险深度的计量单位是%，保险密度的单位为元。模型中各省份保险收入、保险深度与保险密度的数据均来自2004年至2011年《全国统计年鉴》。笔者使用Eviews 7.2建立面板模型^[6]。

为避免模型出现异方差，在模型估计时将各数据进行了对数处理^[7]。实证分析部分首先进行的是机构数量、从业人员数量、营业收入与保费收入间的混合面板模型的估计，即从保险专业中介机构数量、从业人员数量及营业收入三方面衡量其对保险市场是否存在提升规模、扩大供给的作用，其表现在是否对增加保费收入有明显影响^[8]。将全国28个省份的数据进行最小二乘法的回归，并没有考虑个体固定效应或时间固定效应。模型的估计结果如下：

LOG(BFSR) = 6.22801896574 + 0.735961024081*LOG(JGSL)

+ 0.0270144527978*LOG(CYRY)

+ 0.165894377913*LOG(YYSR)

由于混合面板各样本的表达式是相同的，因此全国28个省份的保险专业中介机构的数量、从业人员数量及营业收入规模这三个解释变量与被解释变量保费收入间的关系都遵从上述模型估计结果的表达式。如图1-5所示。

从图1-5来看，第一个和第三个估计系数通过了t检验，即通过了显著性检验，这表明保险专业中介机构的数量及营业收入量是影响保险收入的一个非常重要的因素。但第二个估计系数没能通过t检验，即这一估计结果并不具有显著性，表明通过混合面板模型估计无法从数据上得出保险专业中介机构的从业人员数量是增加保费收入的重要影响因素。两个通过显著性检验的系数的经济含义表明，当保险专业中介机构数量每增加1%，保费收入就多增加0.7360%；保险专业中介机构的营业收入每增加1%，保费收入就多增加0.16597%。从中可以看出，保险专业中介机构在整体数量方面比营业收入规模更能够增加保费收入量，但中介机构的从业人员数量可能并不是影响保费收入的重要变量。此外，输出结果也可以表明，混合模型的拟合程度较低，R2及调整后的R2数值在68%左右，并且模型可能存在比较严重的正自相关性，因此可以考虑个体固定效应模型是否能解决正自相关性，以便能够更加贴切地拟合解释变量与被解释变量间的关系。

图1-5　以保费收入衡量保险市场下的混合面板输出结果

（2）以保费收入衡量保险市场下的个体固定效应面板模型

对于模型应当建立固定效应模型还是随机效应模型，需要进行Hausman检验和F检验。而Hausman检验和F检验都表明，全国面板数据更适宜建立固定效应模型。Hausman检验和F检验的输出结果为图1-6和图1-7。

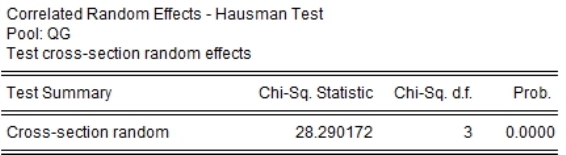
图1-6　Hausman检验输出结果

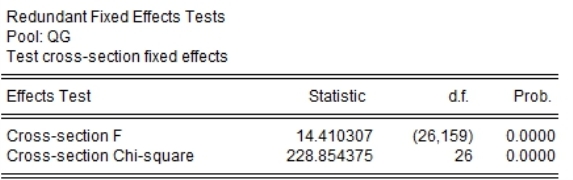
图1-7　F检验输出结果

下面改变混合面板模型，加入个体固定效应也就是建立变截距模型。个体固定效应模型使各省份保费收入与保险专业中介机构数量、从业人员数量及营业收入间的回归关系不再能够以同一个回归表达式体现，而是每个省份都有一个独立的表达式反映三个解释变量与被解释变量的关系，并且个体固定效应的特点是不同个体间的解释变量（常数项C除外）都相同，但截距项即常数项C是不同的，用Eviews回归的模型结果如下：

LOG(BFSR) i = αi+ 7.28971726259 + 0.0966499488282*LOG(JGSL) i

+0.116809041231*LOG(CYRY) i

+ 0.306272782399*LOG(YYSR) i

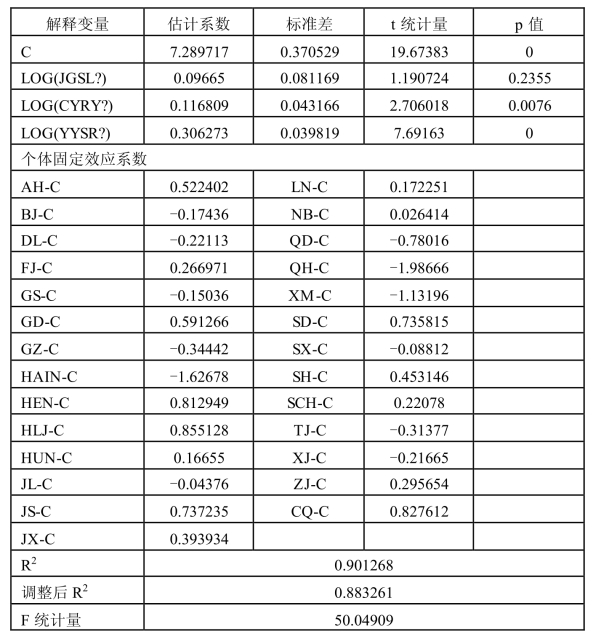
表1-5是个体固定效应面板模型的输出结果。

表1-5中，αi表示不同省份的个体固定效应系数。由于篇幅限制，在此无法将所有28个省份样本的回归表达结果完全列出。通过输出结果可以发现，个体固定效应面板模型的拟合程度系数R2及调整后的R2都上升到了0.9左右，并且自相关（DW）值也有所改善，因此可以说，从输出结果上看个体固定效应模型也优于混合模型。

上述个体固定效应面板模型表明：第一，从业人员数量与营业收入对保费收入的影响系数通过了显著性检验，但机构数量对保费收入的影响未能通过显著性检验；第二，常数项的差别，在个体固定模型中，不同个体样本会有一个“额外”系数，以加减共同系数C得到与不同个体相匹配的真正的截距项，输出结果表明北京、大连、甘肃、贵州、吉林、青岛、青海、厦门、天津、新疆等个体常数项为负数，因此需要从共同常数项中减去相应的个体常数，而其他省份的则为正数，需要在共同常数项的基础上增加相应的个体常数，因此不同的截距常数项就把28个省 份个体分为了两部分，并且这些省份中，经济与保险市场不发达的省份占了绝大多数^[9]，因此，在后文的分析中将发达程度不同的保险市场分开论证是必需的；第三，关于回归系数值的含义，个体固定效应面板模型的输出结果表明，当保险专业中介机构从业人员数量每增加1%，保费收入就多增加0.6811%，保险专业中介机构的营业收入每增加1%，保险深度就多增加0.3063%。无论是输出结果还是F检验与Hausman检验，个体固定效应面板模型更为合适，因此我们更倾向于接受个体固定效应面板模型的结果，认为保险专业中介机构的从业人员数量及营业收入规模的提升有助于保费收入的提高。

表1-5　个体固定效应面板模型输出结果（一）^[10]

（3）以保险深度衡量保险市场下的个体固定效应面板模型

上述两个面板模型是以保费收入衡量的保险市场是否得到了提升与发展，但保费收入并不是衡量保险市场发展程度的唯一指标，保险深度与保险密度由于加入了各省份的国民收入总值及人口因素，因此可以更加准确地衡量保险市场的发展程度，所以接下来就以保险深度为被解释变量，仍以机构数量、从业人员数量、营业收入为解释变量建立面板模型。

通过F检验与Hausman检验表明以保险深度为被解释变量的模型也是更适用于建立个体固定效应面板模型的。图1-8和图1-9为Hausman检验与F检验的输出结果。

图1-8　Hausman检验的输出结果

图1-9　F检验的输出结果

因此建立个体固定效应面板模型即变截距面板模型，得到每个省份的不同的表达式，但每个个体样本的解释变量的回归系数是相同的，用Eviews回归的结果如下：

LOG(BXSD)i =αi+ 0.606738830342 - 0.0710215271018*LOG(JGSL) i

+ 0.0417252561485*LOG(CYRY) i

+ 0.080683325024*LOG(YYSR) i

表1-6为个体固定效应模型的输出结果。

表1-6　个体固定效应面板模型输出结果（二）^[11]

表1-6中，αi表示不同省份的个体固定效应系数。输出结果表明个体固定效应面板模型的拟合程度系数R2及调整后的R2都上升到了0.8以上，该面板模型的解释能力增强了，DW值也有所改善。个体固定效应面板模型的三个回归系数结果都通过了显著性检验，这表明保险专业中介机构数量、从业人员数量与营业收入三者都是影响保险市场保险深度的重要解释因素。从回归结果上看，当保险专业中介机构从业人员数量每增加1%，保险深度就提升0.0417个百分点；保险专业中介机构的营业收入每增加1%，保险深度就提升0.0807个百分点；但保险专业中介机构数量对保险深度的影响系数结果是负值，即保险专业中介机构数量每增加1%，保险深度就下降0.0710个百分点，这一结论明显与前面的理论假设和上面两个面板模型的结论相违背^[12]。

个体固定效应面板模型使每一样本个体具有不同的截距项，输出结果表明，福建、广东、贵州、海南、河南、湖南、吉林、江苏、湖北、青岛、青海、山东、天津等13个省份的个体截距项低于其他省份，这与上一个体固定效应里由于截距项的不同，将全部个体分为两部分的结果十分相似。由于Hausman检验、F检验及输出结果都表明个体固定效应面板模型更为合适，因此我们认为保险专业中介机构的从业人员数量及营业收入规模的提升有助于保险深度的提高，而这一结论与以保费收入作为被解释变量的结论是非常一致的。

（4）以保险密度衡量保险市场下的个体固定效应面板模型

上述两个面板模型是以保险深度衡量的保险市场是否得到了提升与发展，下面以加入了人口因素的保险深度指标作为被解释变量，仍以机构数量、从业人员数量、营业收入为解释变量建立面板模型。

首先仍是通过Hausman检验和F检验来判断应当建立固定效应模型还是随机效应模型。Hausman检验和F检验的检验结果如图1-10和图1-11所示。

(www.xing528.com)

图1-10　Hausman检验的输出结果

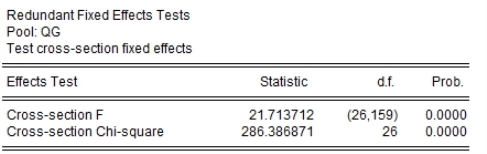
图1-11　F检验的输出结果

根据图1-10和图1-11分析得出，Hausman检验结果表明应当建立随机效应模型，但F检验表明应该建立固定效应模型。笔者通过比较两种面板模型，发现个体固定效应模型的拟合程度系数R2及调整后的R2都上升到了0.8以上，比随机效应模型的R2及调整R2（都保持在0.35左右）高出很多，表明个体固定效应面板模型具有更强的解释能力，并且DW值也有所改善，因此还是建立固定效应面板模型更为合适。

个体固定效应即变截距模型的输出结果为表1-7。

表1-7　个体固定效应面板模型输出结果（三）^[13]

续表

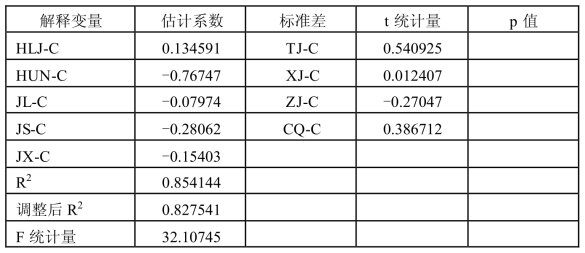
因此将得到每个省份的不同的表达式，但每个个体样本的解释变量的回归系数是相同的，回归模型的结果如下：

LOG(BXMD)i = αi + 4.22091185876 + 0.0858776460469*LOG(JGSL) i

+ 0.100989455956*LOG(CYRY) i

+ 0.293130617518*LOG(YYSR) i

式中αi表示不同省份的个体固定效应系数。输出结果表明保险专业中介机构从业人员数量与营业收入两个解释变量的回归系数结果都通过了显著性检验，因此二者是影响保险市场密度的重要解释因素，但保险机构数量从模型结果上看并不是提升保险市场密度的重要解释变量。回归系数的经济含义表明，当保险专业中介机构从业人员数量每增加1%，保险密度就提升0.1010个百分点；营业收入每增加1%，保险密度就提升0.2931个百分点，这一结论明显与前面的理论假设和上面两个个体固定效应面板模型的结论都是相一致的。

个体固定效应面板模型的系数αi使每一样本个体具有不同的截距项。输出结果表明，北京、大连、福建、黑龙江、宁波、广东、新疆、上海、天津、浙江、重庆等11个省份的个体截距项高于其他省份，并且可以明显发现这些省份中大部分是保险专业中介市场较为发达的地区，因此更加有力地验证了不同保险专业中介机构的发展程度对保险市场的影响程度可能不同，从而为后文按照发达程度将保险专业中介市场划分为两个区域进行比较提供了依据。

因此，保险专业中介机构的发展的确是扩大保险市场、增加保险供给的重要提升因素，并且保险专业中介的从业人员数量及保险专业中介机构营业规模是增加保费收入，提升保险市场保险深度与保险密度的最为主要的影响因素，从而在理论分析部分最后提出的理论假设1和理论假设2得到了证明。

4. 分地域的面板模型

上面是以全国28个省份的保险专业中介机构的数据为总体考虑其对保险市场的作用。下面为了验证理论假设3，将28个省份的个体样本划分为两个区域，将其定义为保险专业中介机构的发达区域及欠发达区域，以两个面板模型不同的回归结果验证不同发展程度的保险专业中介机构对保险市场的提升作用程度可能也不同。我们以2010年的各省份保险专业中介机构的营业收入除以保费收入的结果作为衡量保险专业中介机构发达程度的排序标准，并取前18个省市区及单列市作为保险专业中介机构发达区域的个体样本，它们分别是北京、海南、青岛、广东、天津、四川、青海、厦门、陕西、湖南、辽宁、山东、上海、吉林、福建、浙江、江苏、大连，为方便描述，我们将其定义为面板A；剩下的10个省份作为保险专业中介机构欠发达区域的个体样本，包括新疆、甘肃、重庆、黑龙江、河南、宁波、安徽、云南、贵州、江西，为方便描述，我们将其定义为面板B。

下面我们仍然顺次以保费收入、保险深度、保险密度为被解释变量，以保险专业中介机构数量、从业人员数量及营业收入作为解释变量建立面板模型^[14]。

（1）以保费收入衡量保险市场的面板模型

通过Hausman检验和F检验，都表明建立个体固定效应面板模型更为合理，具体检验结果见表1-8^[15]，并且个体固定效应面板模型能够显著提高回归的拟合程度，并在一定程度上解决面板模型的自相关问题，因此下文的三组面板模型都将以个体固定效应面板模型的输出结果为准，进行保险专业中介机构发达区域与欠发达区域的比较，到时不再赘述检验结果与理由。

表1-8　Hausman检验和F检验输出结果

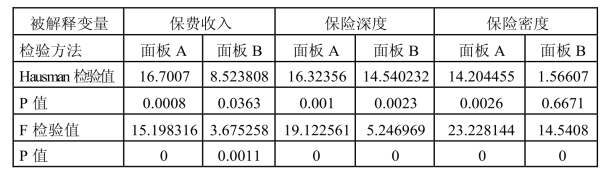
保险专业中介机构发达区域即面板A的回归结果如图1-12所示。

图1-12　面板A个体固定效应面板模型回归结果（一）

图1-12表明，保险专业中介机构的从业人员数量和营业收入规模这两个解释变量的回归系数通过了显著性t检验，表明其是影响保费收入的重要影响因素，但机构数量没能通过显著性检验。其经济意义表现在，当保险专业中介机构从业人员数量每增加1%，保费收入就提升0.2517%；保险专业中介机构的营业收入每增加1%，保险密度就提升0.2539%。

我们再来看保险专业中介机构欠发达区域即面板B的回归结果，以进行比较。如图1-13所示。

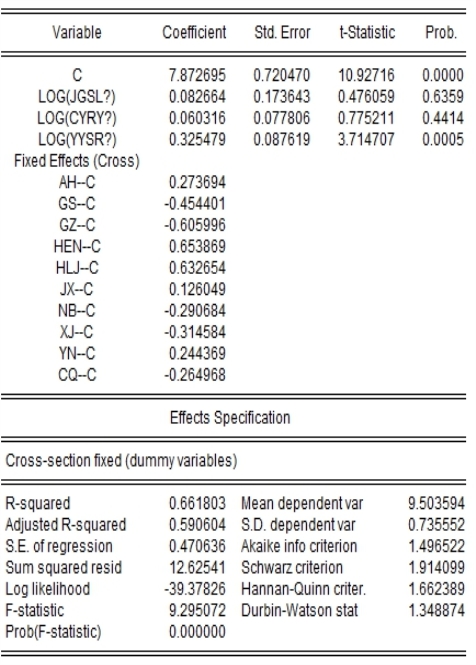
图1-13　面板B个体固定效应面板模型回归结果（一）

面板模型B的输出结果图1-13表明，只有保险专业中介机构的营业收入这一解释变量通过了显著性检验，而机构数量和从业人员数量都未能通过；并且保险专业中介机构的营业收入每增加1%，保险密度就提升0.3255%。

对比两个面板模型很容易发现，机构数量并不是影响保费收入的重要因素，这与上文以保费收入作为被解释变量的全国面板模型得出的结论是一致的，但对于从业人员数量与保险专业中介机构的规模是不是影响保费收入的重要因素，在发达保险专业中介市场与欠发达保险专业中介市场上出现了明显的差异。发达保险专业中介市场面板数据得出的结论与上文全国面板模型得出的结论是一致的，但欠发达保险专业中介市场的面板模型结果并不能印证保险专业中介人员的数量增加能够提升保费收入，并且对于欠发达保险专业中介市场来说，其营业规模给保费收入带来的正向影响也大于发达保险专业中介市场。出现这一现象的原因很可能在于，欠发达保险专业中介机构并未能形成影响保险市场需要的重要力量，因此在数据上无法通过显著性检验。

（2）以保险深度衡量保险市场的面板模型

发达保险专业中介市场即面板A的回归结果如图1-14所示。

从图1-14可以看出，保险专业中介机构的数量、从业人员数量和营业收入规模这三个解释变量的回归系数通过了显著性t检验，表明这三个变量都是影响保费收入的重要影响因素，回归系数的经济意义表现在，当保险专业中介机构数量每增加1%，保险深度就下降0.0884个百分点^[16]；当保险专业中介机构从业人员数量多增加1%，保险深度就提升0.0820个百分点；保险专业中介机构的营业收入每增加1%，保险密度就提升0.0549个百分点。

图1-14　面板A个体固定效应面板模型回归结果（二）

我们再来看欠发达保险专业中介市场即面板B的回归结果，以进行比较。如图1-15所示。

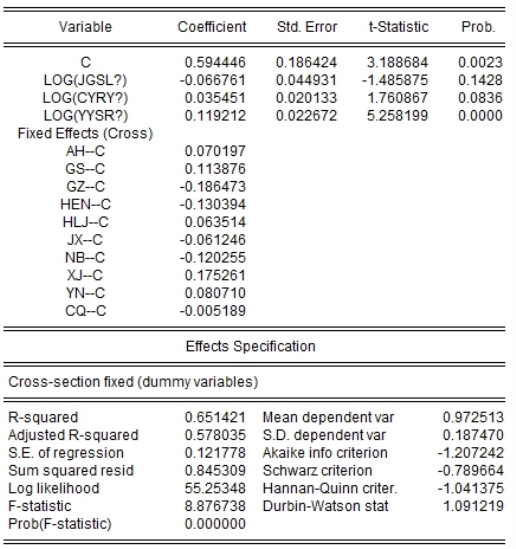
图1-15　面板B个体固定效应面板模型回归结果（二）

面板模型B的输出结果表明，只有保险专业中介机构的营业收入这一解释变量通过了显著性检验，而机构数量和从业人员数量都未能通过；并且保险专业中介机构的营业收入每增加1%，保险深度就提升0.0354个百分点。

对比两个面板模型很容易发现，机构数量并不是影响保险市场深度的重要因素，这与上文以保费收入作为被解释变量的全国面板模型得出的结论是一致的，但对于从业人员数量与保险专业中介机构的规模是不是影响保险市场深度的重要因素，在发达保险专业中介市场与欠发达保险专业中介市场上出现了明显的差异。发达保险专业中介市场面板数据得出的结论与上文全国面板模型得出的结论是一致的，但欠发达保险专业中介市场的面板模型结果则并不能印证保险专业中介人员的数量增加能够提升保险市场的保险深度，并且对于欠发达保险专业中介市场来说，其营业规模给保险深度带来的正向影响也大于发达保险专业中介市场。

（3）以保险密度衡量保险市场的面板模型

发达保险专业中介市场即面板A的回归结果如图1-16所示。

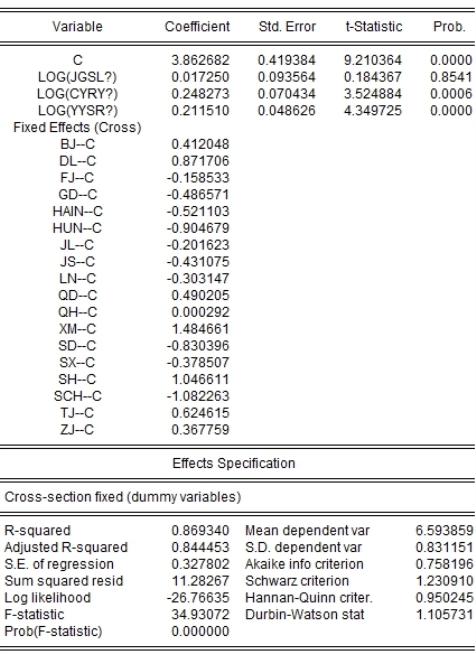
图1-16　面板A个体固定效应面板模型回归结果（三）

保险专业中介机构从业人员数量和营业收入规模这两个解释变量的回归系数通过了显著性t检验，表明其是影响保费收入的重要影响因素，但保险专业中介机构数量的回归系数没能通过显著性检验。通过显著性检验的回归系数的经济意义表现在，当保险专业中介机构从业人员数量多增加1%，保险密度就提升0.2483个百分点；保险专业中介机构的营业收入每增加1%，保险密度就提升0.2115个百分点。

我们再来看欠发达保险专业中介市场即面板B的回归结果，以进行比较。如图1-17所示。

图1-17　面板B个体固定效应面板模型回归结果（三）

面板模型B的输出结果表明，只有保险专业中介机构的营业收入这一解释变量通过了显著性检验，而机构数量和从业人员数量都未能通过；并且保险专业中介机构的营业收入每增加1%，保险深度就提升0.3830个百分点。

对比两个面板模型很容易发现，机构数量并不是影响保险市场密度的重要因素，这与上文以保费收入作为被解释变量的全国面板模型得出的结论是一致的，但对于从业人员数量与保险专业中介机构的规模是不是影响保险市场深度的重要因素，在发达保险专业中介市场与欠发达保险专业中介市场上出现了明显的差异。发达保险专业中介市场面板数据得出的结论与上文全国面板模型得出的结论是一致的，但欠发达保险专业中介市场的面板模型结果并不能印证保险专业中介人员的数量增加能够提升保险市场的保险密度，并且对于欠发达保险专业中介市场来说，其营业规模给保险密度带来的正向影响也大于发达保险专业中介市场。

总结上述三组面板模型，我们可以得出结论，保险专业中介机构数量并不是提升保险市场规模与发展的重要因素，这与全国面板数据得出的结论也是相一致的。与全国面板模型结论不同的是，保险专业中介机构欠发达区域的从业人员数量都不是影响保险市场发展指标的重要因素，但在保险专业中介机构发达区域则表明这一因素是重要的影响因素。这一结论表明，保险专业中介机构的发达程度不同，其对保险市场的影响也不同。由此，我们通过两个面板模型即面板A和面板B证明了理论假设3：保险专业中介机构不同的发展水平对保险市场的需求与质量影响不同；保险专业中介机构的发达程度越高，其对保险市场的提升作用越大。