期望值计算步骤与标准差

（一）期望值的计算公式

期望值也称数学期望，它是随机事件的各种变量与相应概率的加权平均值。它代表了不确定性因素在实际中最有可能出现的值。

随机变量可分为离散型随机变量和连续型随机变量。项目分析中，任一不确定性因素的变化一般均为有限次数，故在分析计算期望值时都使用离散型随机变量。其期望值的计算公式为

式中：E（X）——随机变量的期望值；

i——随机变量的序数，i=1，2，…，n；

X——随机变量值；

P——随机变量发生的概率。

（二）期望值的计算步骤

1.列出项目各种状况的指标值以及在不确定因素作用下各随机变量的概率分布。

设某一投资项目在市场需求变化的情况下存在如表11-2所示的资料：

表11-2

2.根据概率分布计算项目指标的期望值。(www.xing528.com)

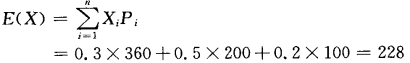
3.计算显示期望值稳定性的标准差和变异系数。

标准差的计算公式为

式中：σ—标准差；

Pi——第i次事件发生的概率；

Xi——第i次事件发生的变量值。

上例的标准差为

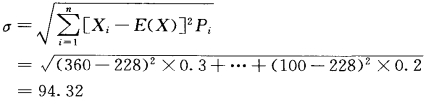
这一指标表示事件发生的变量与数学期望值的偏离程度。指标值越小，说明实际发生的可能情况与期望值接近，期望值的稳定性也越高，项目风险就越小，反之亦然。因此，一个好的项目应该具有较高的期望值和较小的标准差，但应该看到，标准差是一个绝对值指标，它适用于具有相同期望值的不同项目的风险的分析。如果不同项目具有不同的期望值，这时就要利用变异系数进行分析。

变异系数的计算公式为

这个公式的实质是单位期望值所承担的标准差，显然，它消除了由于不同项目具有不同期望值，从而难以进行比较分析的问题。一般而言，变异系数值越小，项目的相对风险越小，反之亦然。