资金时间价值与复利计算公式 - 投资项目评估

（一）资金时间价值的换算

由于资金时间价值的原因，相同数额的货币资金在不同的时点，其经济价值是不相等的；相反，在不同时点的不同数额的货币资金可能是经济等值的。对项目而言，投资往往在前，而收支发生在后，为比较项目收支，必须将不同时间发生的收支额，以资金时间价值换算为统一时点的相当值，才能进行比较。这一过程称为资金时间价值的换算。这是计算项目经济效益和进行经济评价时首先考虑的问题。

资金时间价值的换算包括：（1）现值计算，即将未来时点上的收支换算为某一较早时点上的相当值的方法；（2）终值计算，即把任一较早时点发生的收支换算为未来某一时点的相当值的方法；（3）年值计算，即把任一时点上的价值换算为一系列相等的年相当值。同样，也可把年值换算为某一时点的现值或终值。

为简化上述计算，人们推导了复利计算的基本公式，计算了常用复利系数的数值并编成表格以备查用。美国工程经济协会1975年拟定了复利系数的标准名称与符号，现已被许多国家所采用。下面根据该标准介绍几个常用的复利公式。

（二）普通复利计算公式

在下面的复利计算公式推导中，我们统一用下面的符号表达现金流量：

P——现值；

i——实际利率，按计息期计算的利率；

r—名义利率，即年利率；

n——计算复利的期数（年、季、月、周等）

F—终值或未来值，即发生在现在或未来的现金流量相当于未来时点的价值；

A——年值或年金，即连续发生在一定周期每期末资金的等额系列值；

G——等额递增（递减）的现金流。

为了更加清楚，在复利公式推导计算时，我们将借助前面提到的现金流量图。

1.一次支付终值复利公式

已知期初投入的现值为P，利率i，求n期末的终值F。其现金流量图如图2-3。其公式为

式中（1+i）n称一次支付终值系数，记作（F/P，i，n），可直接查复利系数表得到。

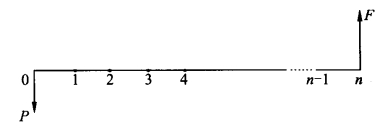
图2-3　P←→F现金流量图

公式推导：本金P在第1年末的利息为Pi，第1年末的本利和为

F1=P+Pi

第2年末的本利和为

依此类推，第n年末的本利和为

【例2-5】　若现存款1000元，设利率为8%，则第2年末取回多少？

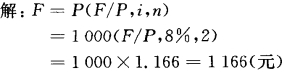
2.一次支付现值公式

这是已知终值F，求现值P，可由式（2-3）导出：

式中1/（1+i）n称为一次支付现值系数，记作为（P/F，i，n）。

【例2-6】　为了两年后得到1166元，按年利率8%计算，现在必须存入多少？

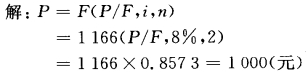
要特别指出的是，在上面的两个公式中，我们始终用到年（期）末的数据，这是我们在复利公式推导和使用时必须注意的，后面的公式也使用年（期）末的数据。

3.等额支付终值公式

若每期期末支付等额金额A，在年利率i的情况下，就不需要一年一年地计算其现值或终值，可以采用等额支付终值、现值公式。先来看等额支付终值公式。

若已知年金A，利率i，求n期末的终值F，其现金流量图如图2-4。其公式为

式中［（1+i）n-1］/i称为“等额支付终值系数”，记作（F/A，i，n）。

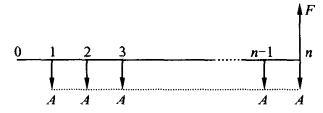
图2-4　 A←→F现金流量图

公式推导：从图中可以看出，等额支付序列可视为n个一次支付的组合，F值等于n个现金流中每个A的未来值之和，即

上式两边同乘（1+i）得

（2-7）式减去（2-6）式得

则

【例2-7】　每年末存入银行100元，假如银行按复利计息，年利率8%，6年后可得多少钱？

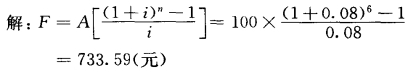
4.等额支付偿债基金公式

这是已知n期末的终值F，求n期末的等额系列金额A，如图2-4。可由式（2-5）导出：

式中i/［（1+i）n-1］称为“等额支付偿债基金系数”，记作（A/F，i，n）。

【例2-8】　某公司计划5年后购进一台自动装置，需投资10 000元，为此决定从今年起每年提存等额年金，作专用基金存入银行，若利率为10%，问需要每年储存多少？

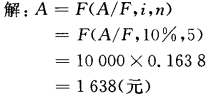
5.等额支付现值公式

已知n期内每期等额金额A，利率i，求现值P，如图2-5。由F=P（1+i）n和F=A［（1+i）n-1］/i，得

式中称为“等额支付现值系数”，记作（P/A，i，n）。

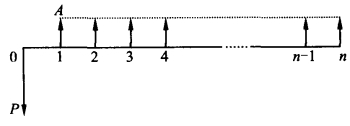
图2-5　P←→A现金流量图

【例2-9】　如果想在今后8年中，每年年末得到资金200元，假设年利率5%，现在应该一次投入多少钱？(www.xing528.com)

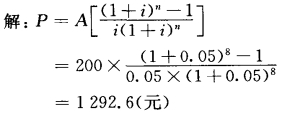
6.等额支付系列资本回收公式

这是已知现值P，求n期内每期末的等额现金值A，如图2-5。可由式（2-9）导出：

式中称为“等额支付系列资本回收系数”，记作（A/P，i，n）。

【例2-10】　某公司向银行借款15000元购一台设备，年利率10%，规定10年内以等额偿还，求每年应偿还额。

（三）等差支付复利计算公式

1.等差递增（减）序列现值公式

在经济分析中，常遇到某些现金流量每年均以一定的数量增加或减少，即形成等差的数列。例如，固定资产随着使用年数的增加，维修费用逐年增加，其产量则逐年减少。如果每年的现金流量增加额或减少额相等，则称之为等差序列递增（减）现金流量，此时，n年的收支额可依次表示为A1，A1+G，…，A1+（n-1）G，如图2-6所示。G称为递增（减）量。在计算该类支付情形的现值、终值和年值时，可将问题简化，即将图2-6所示的现金流量看成两个现金流量之和（如图2-7所示），一个为等额支付序列现金流量，一个为递增（减）支付序列现金流量。前一种情形前面已经介绍，后一种情形是已知等额递增（减）量为G，求n期的现值P。

公式如下：

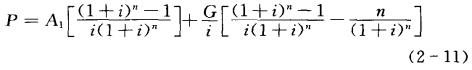
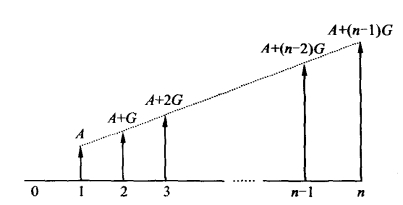
图2-6　等差序列递增现金流量图

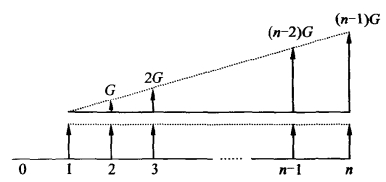
图2-7　等差支付现金流量分解图

式中称为等差支付现值系数，记作（P/G，i，n）。

公式推导（只要推导（2-11）式的后半部分）：

等式两边同乘以（1+i），得

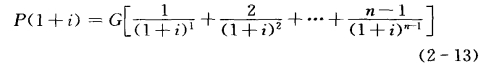
（2-13）式减去（2-12）式，得到

合并得到

故而

2.等差递增（减）序列终值公式

已知等差递增（减）量为G，求其终值F。将式（2-11）代入式（2-3），可得

式中称为“等差递增（减）终值系数”，记作（F/G，i，n）。

【例2-11】　某公司租赁一批设备，按合同规定，第一年支付租金5万元，以后每年递增2万元，租期5年，年利率5%。若采用一次付款方式，第一年初应付款多少？若为第5年末一次付款，应付多少？如图2-8所示。

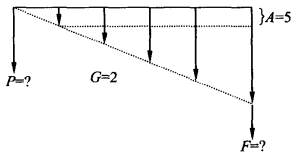
图2-8　［例2-11］图示

解：若年初一次付清，则

若最后一年末一次付清，则

3.等差递增（减）序列年金公式

已知等差递增（减）量G，求年值A。这里只要计算递增（减）G的年金A2即可。公式如下：

式中称为“等差递增（减）年金系数”，记作（A/G，i，n）。

（四）间断等额序列年金的处理

等额序列年金往往是不连续的，而是间断的，而且年金金额及符号也可能不一样，如图2-9所示。

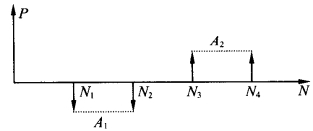
图2-9　间断等额序列年金

间断性产生的原因是多方面的，如项目投产后，要经过一段时间才能达到全部设计生产能力，这段时间内净现金流量逐年增加，并非等额序列。达到设计能力后，经过一定时期后，又要进行技改、改扩建、大修理等措施，这些措施使资金流入量增加，流出量减少，甚至减产和停产。这些措施完成后，生产可达到新的水平。因此，时间N2与N3有间隔，同时资金流量A1与A2也不一定等额。

间断序列年金现值计算方法很重要，在时间价值计算中经常会用到。其一般的方法是分别计算不同的全部年限的年金，再对应相减得到要计算的年金值，具体的计算方法需要因间断的情况而定，譬如如图2-10所示的间断年金，就可以采用减法来计算其现值或终值。如下：

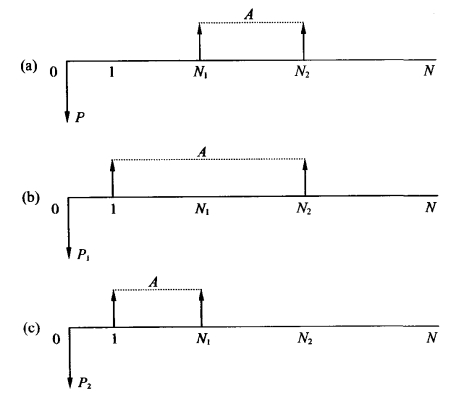
图2-10　间断序列年金计算方法（一）

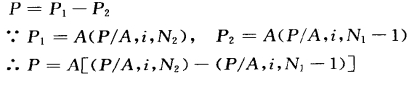
注意上式中P2的年限是（N1-1）。

上面的情形也可以采用其他的方法来解决，如图2-11。

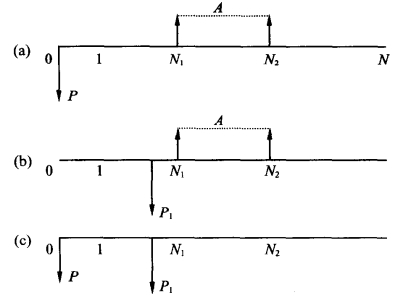
图2-11　间断序列年金计算方法（二）

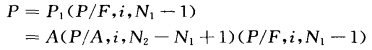
【例2-12】　某项目投资总额（包括建设期利息）为2000万元，投产后第5年开始还贷款，要求在6年内清偿，贷款年利率10%，每年应还贷款多少？

解：现金流量图如图2-12。

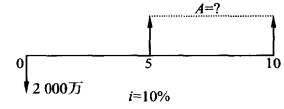
图2-12　［例2-12］图示

需要特别指出的是，在运用这些复利公式计算时，必须符合以下条件：（1）计息周期与复利率周期要一致。（2） P发生在第一期初（t=0），F发生在第n期末（t=n）。（3） A发生在连续几个周期期末，计算期数为n的发生次数。（4）等额递增序列发生在第二期起的每期末，计算期数为递增支付流量发生的次数加1。（5）当问题包括P和A时，P发生在第一个A的前一期；当问题包括F和A时，F与最后一个A同时发生；当问题包括P和G时，P发生在第一个G的前两期；当问题包括A和G时，第一个A发生在第一个G的前一期，最后一个A与G同时发生。