获得优良初估计的方法

SAS计算准确、快速，只要初始估计取得合理，总能通过最优化得到合适的最优参数估计，从而得到合适的模型。但是由最优化理论可知，初估计对迭代的结果影响很大。例如图8-10中，一元非线性函数SSE可能有多个极小值：a=2.2，3.3，4.2，4.9，其中a=4.9是全局最小值点。

图8-10　参数a=2.2，3.3，4.2时SSE极小

初估计取得不好，不仅收敛速度慢，而且可能不收敛到最小值点。如果在图8-10的情形（仅考虑1个待估参数）：初估计取在［1.5，2.5］中任一点，那么最优化结果会得到极小值点是a=2.2；初估计取在［2.9，3.5］中任一点，例如图中初估计为2.9，那么最优化结果会得到极小值点是a=3.3；初估计取在［3.8，4.5］中任一点，那么最优化结果会得到极小值点是a=4.2；只有初估计取在［4，7，5.2］任一点，例如图中初估计为4.7，最优化结果才会得到全局最小值点是a=4.9。具体实例可见8.2.4节的练习题1。好的初估计不仅收敛速度快，而且总能收敛到全局最小值点，因此应当尽量选用好的初估计，好的初估计称为优良初估计。

当对于初估计只有很少信息可用时（如例8.18），可以采用如下初估计选取方法：若参数a可以是任何实数，则取a的初估计0；若参数b可以是任何正数，则取b的初估计1。也可以给每个参数若干个可能的初估计，让SAS从不同搭配的初值中选出最好的一个（残差平方和SSE最小的一个）作为初值去迭代。

获取优良初估计的方法是：（1）利用线性回归模型中某些参数特性选取初估计，如8.2.2节练习题的提示。（2）利用将非线性回归模型化为线性回归模型而用线性回归求出，即对于已知非线性回归模型（式（8-4）），去掉误差项，变成构造另一个方程与它等价，那么线性回归模型的解是非线性回归模型的优良初估计。注意非线性回归模型和线性回归模型因为误差项的不同位置而是不同的模型，见例8.19。

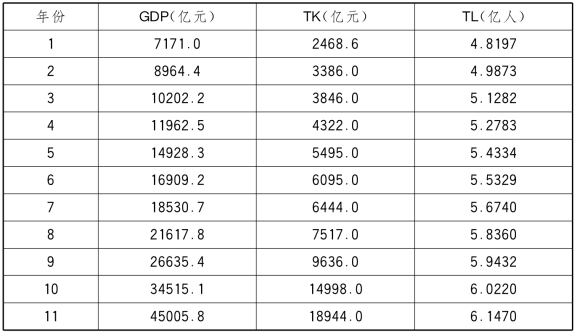
例8.19　某国连续11年的GDP和资金投入（TK）、就业人数（TL）如表8-19所示，它们满足柯布-道格拉斯生产函数模型。试用表中数据拟合柯布-道格拉斯生产函数模型。

表8-19　某国连续11年的GDP、资金投入、就业人数数据

解　由于各种误差的存在，应当考虑非线性回归模型

为了用线性回归近似法求出优良初估计，将柯布-道格拉斯生产函数模型两边取对数化为

它与柯布-道格拉斯生产函数模型等价。令z=log（GDP），k=log（TK），l=log（TL），考虑线性回归模型

用下列程序拟合线性回归模型（式（8-8））：

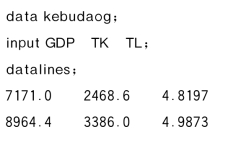
提交程序后得到如下数表：

Parameter Estimates

因为截距是log（a）的估计，取exp（0.25099）=1.285为a的初估计，0.62023为b的初估计，2.37894为c的初估计，采用nlin过程拟合非线性回归模型［式（8-7）］，程序如下：

提交程序后得到如下两张数表：

NOTE：Convergence criterion met.

由上表可见经过5次迭代后最优化过程收敛。

NOTE：An intercept was not specified for this modeI.(www.xing528.com)

由上表可见经验回归方程效果好，表达式是

此例中要注意：原始数据中就业人数是以万人为单位，如果不化为以亿人为单位，就会造成SSE太大，收敛速度慢。例如有的文献中就业人数是以万人为单位，初估计取为a=0.2，b=0.6，c=0.5，则要迭代258次才收敛，而该文献所用软件不精确，因而该文献中算出的是不正确结果，与上面的结果不一样。可在SAS的proc nlin语句中加选项“iter=10000”，就能允许迭代次数达到10000，从而得到正确的结果（见本节练习题）。

有的时候，不能直接将非线性回归模型化为线性回归模型，而要利用模型的特性预先估计一些参数，再将非线性回归模型化为线性回归模型。

例8.20　已知牧草重量y（干重，单位为克）与生长天数t的关系是Gompertz模型

9次观察的数据如表8-20所示。试估计a，b，c的值，并预报第101天牧草的重量。

表8-20　牧草生长资料

解　模型中有3个参数a，b，c，其中a是线性出现的，另两个则是非线性出现的，若取两次对数，则参数b，c变成线性出现的，而a又变成非线性出现的，仍然是非线性模型，仍不好办。为此，可以先估计出a的值。因为曲线y=aexp｛-exp｛b-ct｝｝是S型曲线，自变量t趋于无穷时，y=aexp｛-exp｛b-ct｝｝渐增趋于a，即y=a是渐近线，于是取一个比所有y观测值都大但又大得不太多的数70作为a（渐近值）的初估计。将等式y=aexp｛-exp｛b-ct｝｝两边取两次对数得log（-log（y／70））=b-ct，令v=ln（-ln（y／70）），u=-t，则得到线性回归模型v=b+cu+η。它的截距的估计值即b的优良初估计，自变量u系数的估计值即c的优良初估计。

为此，采用如下SAS程序：

提交程序后得到参数估计表如下：

Parameter Estimates

由此表可见，优良初估计分别是1.48884和0.05601。有了初估计，就能用nlin过程寻求最优解，SAS代码如下：

提交程序后得到如下主要输出：

以上是参数估计表，其中b和c的近似P值都小于0.1，可见b和c都是显著的。所以经验回归方程是

上面是预报值表，可见第101天牧草的重量预计为76.4339克，95%置信区间是（67.6494，85.2184）。

练习题　数据单位取得不好，会造成优化中出现困难，试把表8-19的数据中劳动力人数改为以万人为单位，看看会遇怎样的优化困难，又该如何克服困难。

提示　（1）以a=1，b=1，c=1为初估计，建立程序如下：

提交后优化过程进行不下去（只迭代了5次），原因是SSE太大。将就业人数单位由万人改为亿人，就能进行下去。