用nlin过程进行非线性回归分析—来自《实用SAS基础》

nlin过程采用了最优化的非线性最小二乘法来估计参数，可供选择使用的最优化方法有：最速下降法（梯度法）、牛顿法、高斯（又称为高斯-牛顿）法、麦夸特法和DUD法等。当你选用这些最优化方法之一时，只要在data语句引入选项“method=”，然后加上“gradient”、“newton”、“gauss”、“marquardt”或“dud”之一即可。nlin中默认的最优化方法是高斯法。

nlin过程有3条必要语句：proc nlin，model和parms语句，根据需要还可选用output语句以作预报。以下分别介绍它们。

（1）proc nlin语句。用于调用nlin过程，有两个主要选项：“data=”用于说明回归所用的数据集，如果没有这一项，SAS就采用最近产生的数据集；“method=”用于规定最优化方法，如果没有这一项，SAS就默认采用高斯-牛顿法作为最优化方法。例如，“proc nlin data=wang method=marquardt；”表示对数据集wang中的变量作非线性二乘，最优化方法是麦夸特法。

（2）model语句。用于说明确定性部分，其形式是“model y=f（x1，…，xm，b1，…，bp）；”，其中y表示因变量，x1，…，xm是自变量，b1，…，bp是待定参数，f（x1，…，xm，b1，…，bp）是确定性部分具体形式。例如，“model y=a＊sin（b＊x）+c＊log（z）；”表示回归模型是

其中，y是因变量，x和z是自变量。这点与reg过程不同，reg过程只要列出自变量，无需列出公式。

（3）parms语句。用于给出优化迭代过程的初值。初值可以是唯一的，例如，“parms b1=1.3 b2=0.4 b3=-25；”给出初值b1=1.3，b2=0.4，b3=-2.5；也可给出多个初值，让SAS选择其中最好的，例如“parms b1=10 15 24 b2=3.1 4.2 5.7 b3=2to 4by 0.4；”规定了b1有3种选择即10、15、24，b2有3种选择即3.1、4.2、5.7，b3有6种选择即2、2.4、2.8、3.2、3.6、4，于是b1、b2、b3共有54种不同搭配的初值，SAS从中选出最好的一个（残差平方和SSE最小的一个）作为初值去迭代。在8.2.3节将介绍优良初估计（较好初估计）的选取方法。

（4）output语句。为了得到预测值，可以加上output语句。例如“output out=wang p=yhat l95=yl95 u95=yu95；”指示计算机将预报值存入数据集wang，y预报值命名为yhat，y的95%置信区间下限命名为yl95，95%置信区间上限命名为yu95。

例8.18　对于例8.17，求出a，b和d的估计值，并预测为了有95%的把握不违反交通规则，此人在饮酒后多少小时能驾车出行。

解　取变量c和t分别表示血液中酒精浓度和饮酒后的时间；把表8-18的数据输入为数据集work.alcohal；为了有95%的把握不饮酒驾车，应当求出每一时刻此人血液中酒精含量的95%置信区间。由药物动力学理论知道：a，b和d都是正数，且b＜d，由此初估计取a=1，b=1，d=2。采用高斯-牛顿最优化法。那么可采用程序如下：

提交后得到许多表，其中最主要的是以下3张：

The NLIN Procedure Dependent VariabIe c Method：Gauss-Newton Iterative Phase

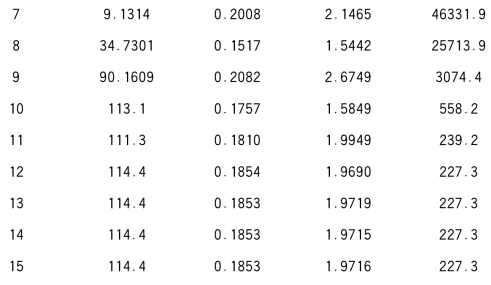
NOTE：Convergence criterion met.

由上表（迭代情况表，表头为Iterative Phase）可见：初始SSE=54277.1；经过15次迭代后，SSE降为227.3，收敛准则满足。参数估计变为=114.4，=0.1853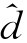，=1.9716。(www.xing528.com)

NOTE：An intercept was not specified for this modeI.

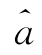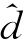由上表可见：近似P值（Approx Pr＞F）小于0.0001，说明近似回归效果好；参数估计是=114.4，=0.1853，=1.9716；a的近似95%置信区间是（104.6，124.1），b的近似95%置信区间是（0.1662，0.2044），d的近似95%置信区间是（1.6505，2.2927）。由于这儿建立的模型是非线性模型，使用的方法是最优化方法，这些估计值（概率）都是近似的。

由上表给出饮酒后27个时刻的血液中酒精浓度预测值、95%置信区间下限（cl95）和95%置信区间上限（cu95）。为了确定什么时间可以开车的概率达到95%，画出95%置信区间上限的时间序列图，并且画一条血液中酒精浓度为20毫克／升的直线。使用以下程序：

提交程序后得到图8-9。

图8-9　某人血液中酒精浓度的95%置信区间上限图

从图中可见饮酒后第11.6小时，此人血液中酒精浓度的95%置信区间上限低于20，因此为了有95%的把握不饮酒驾车，此人应当在饮酒后11.6小时后驾车。当然数学模型与人体真实情况总有差距，但是这种预测饮酒后避免酒驾的方法有很大参考作用。

练习题　表8-16的某国人口数据用时间的二次函数拟合的效果很差，改为拟合Logistic模型。

提示：Logistic模型是生物学、经济学中的重要模型，其表达式是

其中，N（t）是时间t的人口数；t，t0分别表示自变量时间和初始时间；Nm，N0分别表示所能容纳的人口最大数和初始人口数；r表示每10年的自然增长率（r＞0）。共有3个待估参数，都是以非线性出现的。由于数学模型和实际情况总有偏差，假设模型为：

将表8-16中的人口改以百万人为单位，t0=1790。由于Logistic回归的特性——当t趋于正无穷时，N（t）上升至Nm。考虑参数取初估计如下：N0约为3.929；Nm可取为比20.3211略大的数，例如25；正数r取为1。