SAS野点查找与处理法：实用技巧

野点，又称为异常点、反常点，是回归模型中很常见、很有用的概念。发现野点和处理野点是非常必要的。

8.1.7.1　野点概念

首先看一个例子。

例8.13　一般说来个子高的人腿较长。统计9个女孩的身高与腿长，得数据如表8-14所示。试建立由身高预测腿长的经验公式。

表8-14　9个女孩的身高与腿长数据

解　这儿有两个变量，用x记身高，y记腿长，每个女孩的身高和腿长是每个女孩的“观测”，构成1个数据行。以x为横轴，y为纵轴画出图来，则每个人的数据就是平面上的1个点。可用reg过程作回归，同时把9个女孩的身高用plot语句画成散点图，即采用程序如下：

提交程序后得到由这9个观测值画成的散点图及回归方程的直线图，如图8-4所示，其中虚线是经验回归方程（回归直线），“+”代表原始观测值。

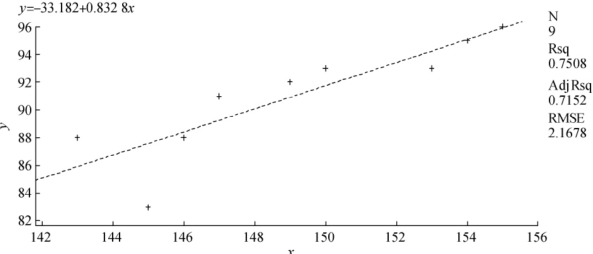
图8-4　观测值的散点及回归方程的直线图

由以上散点图可见，第2个点（x=145，y=83）与回归直线距离较远，这意味着第2位女士的观测值与经验回归方程不符合。第2个观测数据被称为“野点”。

一般地，若某次观测严重偏离回归模型，则称它是野点（outlier）或异常点，也称之为离群数据。同一数据体可能有多个野点。

野点出现的原因有多种，可能是抄写错误，例如某次观测中，y的观测值原本是12.99，相应的数据本应和其他数据协调，但抄写时小数点错写一位，变成了1.299，因而该次观测数据就变成野点了。也可能是某些因子未被考虑，如例8.13中2号女孩可能与其他8位女孩属于不同种族，作回归时种族这一因子就未被考虑。应当把抄错的数据订正，也应当分析其他因子（例如种族）把其他因子加入回归方程。

8.1.7.2　影响分析——发现野点的方法

如何发现野点？当然你应当细心些，并且经常核查数据，这样一来因为书写错误造成的野点就会被及早发现并纠正。在建立模型前也应当检查是否会有其他因子影响回归。但是许多因子不一定事前会被想到，例如身高和腿长公式是否要考虑其他因子（地区）影响，你不一定能想到；也不一定能预先判定什么因子会影响回归效果；在大量抄录数据时也难免出错。因此必须考虑用数学工具查找野点。

检查是否存在野点最简单的方法是画PP图（Probability-Probability plots），在统计软件未普及前，它是由人工把残差在正态概率纸上描出的图形。用reg过程能画残差的PP图。PP图有两个作用：①判断残差是否服从正态分布，如果图中残差的散点图在一直线附近，残差就服从正态分布（回归效果好）；否则就不服从正态分布（回归效果不好）。②判断是否有野点，如果有几个残差的散点太低（接近概率为0的直线）或太高（接近概率为1的直线），说明有的残差太小或太大，对应的点就可能是野点。度量残差太小的标准是散点低于概率为0.05的水平线，度量残差太大的标准是散点高于于概率为0.05的水平线。让SAS画残差PP图的指令是在model语句后加上语句“plot npp.＊r.；”。

例8.14　对于例8.13的数据画残差PP图作并分析。

解　采用如下程序：

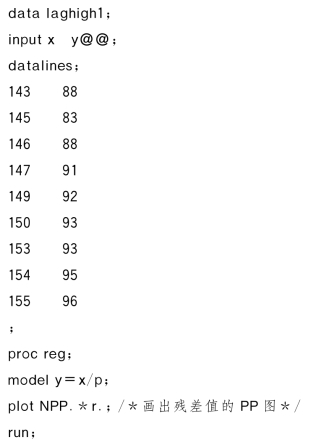
提交后得到的图形如图8-5所示。

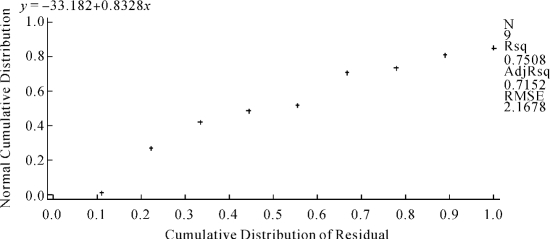
图8-5　女孩腿长数据残差值的PP图

可见各点大体在一直线，但有一个点太接近概率为0的直线（最下方的水平线）。最好在图中画出各点接近的直线，以利于检查各点是否在一直线。为了画该直线需要增加一个数据集，用它指定直线的设置，可以将该数据集命名为work.huazhixian。在画PP图前生成数据集work.huazhixian，再在plot语句中通过选项“annotate=”调用它即可。本例为了画出该直线可用如下程序：

对该程序细节不作介绍。提交该程序后得到图8-6。

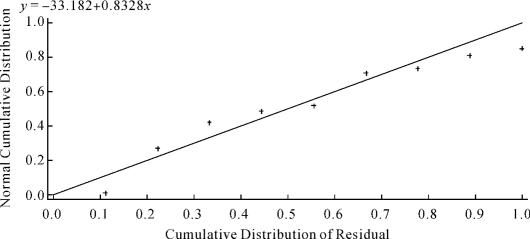
图8-6　女孩腿长数据回归误差PP图

画图找野点的分析方法简单，但是比较粗糙。比较精细的分析方法是计算影响统计量，它属于影响分析。影响统计量测量每次观测对于估计值影响的大小，影响统计量大的观测称为强影响点。野点必是强影响点，但强影响点有可能不是野点。计算影响统计量是影响分析（influence analysis）的重要内容，有关影响分析的理论和方法请看Belsley［1］和韦博成［20］的著作。

影响分析的常用方法之一是数据删除模型（case deletion model）法，也称为数据删失模型法。数据删除模型法是将某次观测删去，分析删去某次观测后所算出的结果与不删除该观测所算出的结果的差异。例如对模型

用观测值

拟合一次，再删去第i次观测，用观测值

拟合一次，比较两次所估计参数的差异，这种方法就是数据删除模型法。

由于影响统计量一般都是随机变量，其分布一般不易得到，只能给出经验准则，用于判别影响统计量是否异常。经验准则不一定绝对正确，某个影响统计量表现异常，不一定表示相应观测值就是野点。因此应当综合考虑几个影响统计量。

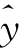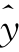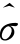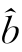设n是样本容量；m是自变量个数；p=m+1是回归模型中待估参数个数；X是设计矩阵；1是yi的预报值，ri=i-yi；hii是帽子矩阵（H=X（X′X）-1 X′被称为帽子矩阵）对角线上第i个元素；2是方差估计值X（i）是删除第i次观测后的设计矩阵；j（i）是删除第i次观测后的bj参数估计；σ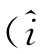）2是删除第i次观测后的方差估计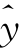；j（i）是删除第i次观测后yj的预报值。

常用影响统计量及其判别准则如下所述，有关细节可见Belsley（1980）。

（1）杠杆值。hii称为自变量第i次观测的杠杆（leverage）。经验上，杠杆大于2（m+1）／n的观测被认为是强影响点，也即第i个点可能是野点。

（2）库克距离（Cook's D）。第i次观测的库克距离是

当Di＜0.5时，认为第i次观测不是强影响点；当Di＞1时，认为第i次观测是强影响点。

（3）学生化残差。第i次观测的学生化残差是

称之为学生化残差，它的绝对值可用来查找强影响点：|rstudenti|＞2时认为第i次观测是强影响点。

（4）协方差比。第i次观测的协方差比是

称之为协方差比。若|covratioi-1|＞3p／n，则认为第i次观测是强影响点。

（5）dffitsi。第i次观测的dffitsi是

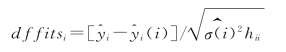
若|dffitsi|＞2则第i个观测是强影响点。

（6）dfbetask，i。第k个参数，第i次观测的dfbetask，i是

其中，Dii是X′X对角线上的第i个元素。若|dfbetask，i|＞则第i次观测是强影响点。SAS对于截距和每个自变量给出dfbetask，i的值。

用SAS计算影响统计量可采用reg过程，在model语句中加上选项r和选项influence后，计算机就会计算库克距离、学生化残差、协方差比、dffitsi和dfbetask，i。

例8.15　研究某市经济开发区经济发展与招商投资的关系。表8-15列出了某时段招商注册资本在5亿元到50亿元的15个开发区的数据，其中x1为某时段累计招商数目，x2为招商企业注册资本（单位为百万元），因变量y为销售收入（单位为百万元）。试作影响分析。

表8-15　某市经济开发区经济发展与招商投资数据

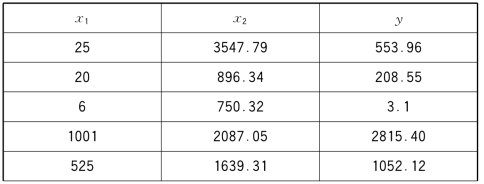
续表8-15

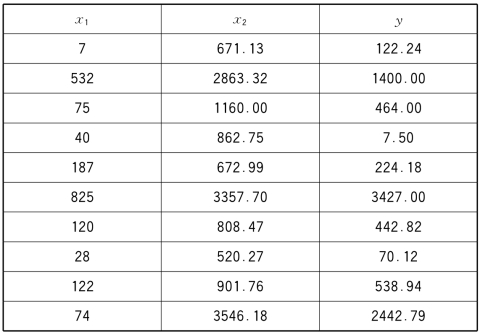
解　对于例8.15采用如下程序：(www.xing528.com)

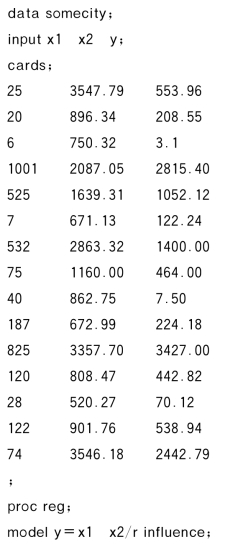
输出的结果中有影响统计量表如下（为了简单，略去其中图形，把过宽的表分成两张表）：

第1张

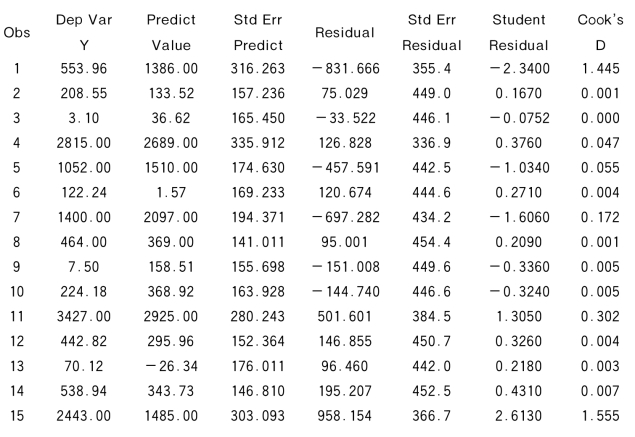
上表的最后1列（列名为Cook's D）给出库克距离，由于第1次和第15次观测的库克距离大于1，估计第1次和第15次观测是强影响点。

第2张表由上表可见：

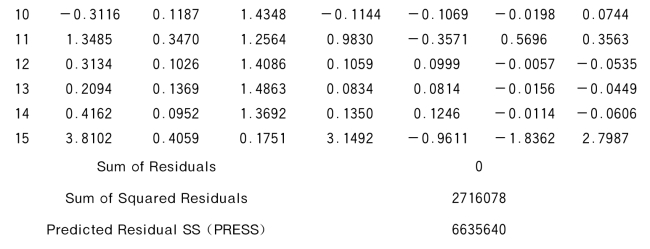
（1）第2列（列名为Rstudent）给出学生化残差rstudent，可见第1次和第15次观测的rstudent绝对值大于2，所以第1次和第15次两次观测有较强影响。

（2）第3列给出杠杆值，第1次、第4次和第15次观测的hii＞2＊3／15=0.4。

（3）第4列（列名为CovRatio）给出协方差比covratio，第1次、第4次和第15次观测的|covratioi-1|＞3p／n=0.6。

（4）第5列（列名为Dffits）给出dffits，其中第1次、第11次和第15次观测的dffits绝对值大于=0.894。

（5）第6列（列名为Intercept Dfbetas）给出截距的dfbetas，其中第1次和第15次观测的dfbetas绝对值大于2／=0.516。

（6）第7列（列名为x1Dfbetas）给出x1的dfbetas，其中第1次、第11次和第15次观测的dfbetas绝对值大于2／=0.516。

（7）第8列（列名为x2Dfbetas）给出x2的dfbetas，其中第1次和第15次观测的dfbetas绝对值大于2／=0.516。

综合以上情况，怀疑第1次和第15次观测是异常点。

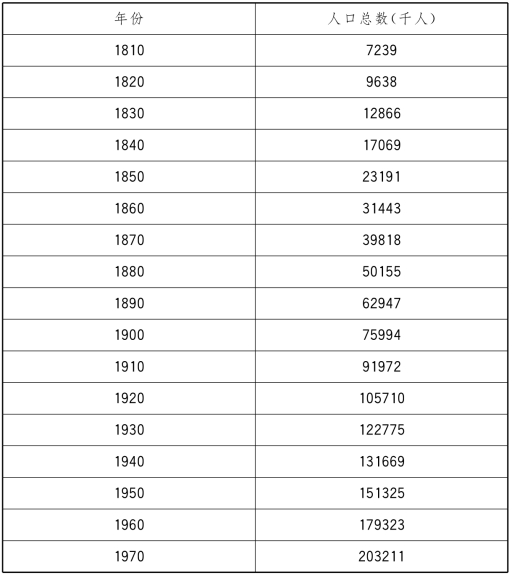
练习题　1781至1970年，每隔10年某国调查人口一次，总数如表8-16所示。试以统计时间（单位为年）及其二次方作回归，查找强影响点。请注意：每10年统计一次，只有一个数据。

表8-16　某国人口数（1790—1970年）

续表8-16

8.1.7.3　野点处理方法

找出强影响点后加以分析就能找出野点。怎样消除野点的不良作用？可以采用如下一些处理野点的方法：

（1）如果经过核实，发现个别数据登录错误或测量错误，就应当把这些数据删除或更改。例如对于例8.13可以删去第2位女孩的观测数据，然后重新拟合模型。

（2）如果有多个野点，发现出现野点的原因是测量方法不好，或者仪器失灵，造成误差大，就应当更改仪器或测量方法。

（3）如果发现缺少重要自变量，就应当增加自变量。例如分析女孩腿长与身高关系时发现两个民族各有多人，因而出现野点，那么就应当加进民族这一因子，简单的做法是分段回归法。下面举一个分段回归的例子（例8.16），虽然用影响分析不能查出强影响点，但是从图形看出显然应当增多自变量。

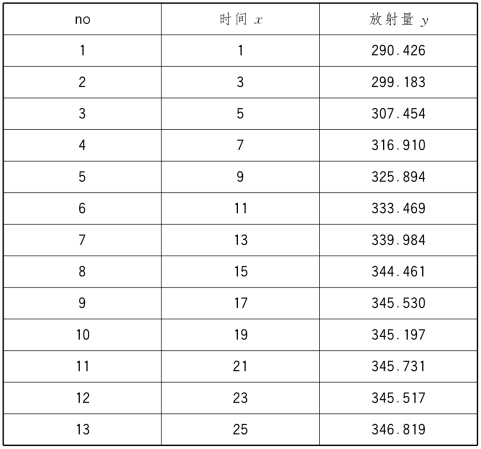
例8.16　表8-17是时间x与放射量y的数据，根据该数据建立因变量y和自变量x的线性回归模型。

表8-17　时间x与放射量y的数据

解　用下列程序画出散点图：

得到的图形是图8-7。

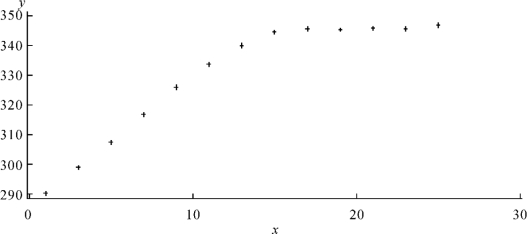
图8-7　放射量-时间散点图

从图8-7可见，放射量-时间散点图不是近似于直线，而是近似于折线：在x=13附近发生转折，假设x=13前数据近似于一条斜线，x=13后数据近似于另一条斜线。如果直接以x为自变量作一元线性回归的话不合理。为此引进3个自变量x1，x2，x3，分别表示两段斜线部分数据。因为折线在x=13附近转折，变量x1表示在时间x=13前的斜线部分自变量的值：当x小于或等于13时，x1等于x；x大于13时，x1等于0。变量x2表示x=13后的斜线部分自变量的值：当x小于或等于13时，x2等于0；x大于13时，x2等于x。x3表示第二段斜线与第一段斜线截距的单位差：x小于或等于13时，x3等于0；x大于13时，x3等于1。也即

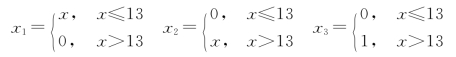
以x1，x2，x3为自变量，y为因变量作回归，建立如下程序：

提交程序后得到的结果中主要有以下两张数表：

Parameter Estimates

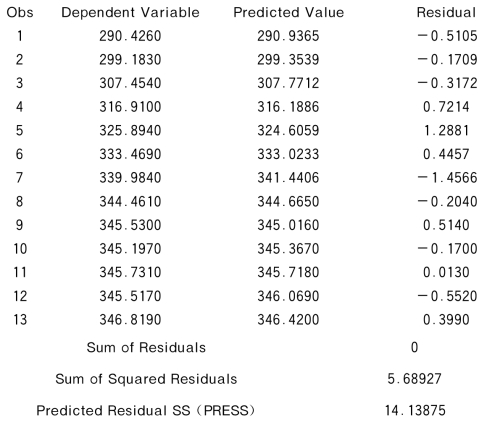
Output Statistics

由第一张表（参数估计表，表头是Parameter Estimates）可见，所有参数都显著，经验回归方程是（这样的回归也称为分段回归）

该表达式的含义是：当x在0与13之间时，经验回归方程是

当x大于13时，经验回归方程是

由第二张表（预报表，表头是Output Statistics）表可见，对原有数据，残差（预报误差）不大。

注意1　由于回归模型中有截距参数存在，0至13那一段上不需要另外设置变量来决定这一段的截距；第二段上则需要用变量的系数来表示第二段与第一段截距的差距。

注意2　如果直接用前7个数据（x＜=13的数据）直接作线性回归，也能得到第一段的斜率和截距；直接用后6个数据（x＞13的数据）直接作线性回归，也能得到第二段的斜率和截距。但是两次计算所得的方差估计值分别是由7和6个数算出的，不稳定；而由程序中13个数据计算所得的方差估计值比较稳定。

（4）模型选用错误，就应当修改模型。

例如对于8.1.7.2节的练习题，采用二次多项式模型，程序如下：

提交程序后发现多个野点。看来模型不好，改用Logistic模型后（见8.2.2节的练习题），各年的残差（预报误差）都很小了。

（5）因为野点对于建立回归模型有一定参考作用，有时不希望把它删除。不删除野点但又能减少野点影响的另一个办法是LAD回归，见后文例8.21。

练习题　根据表6-3的数据，建立分段回归，以身高为自变量，体重为因变量，按不同地区建立分段线性回归模型（按性别分为两组）。