解决共线性问题：岭回归和主成分回归

对于一个多元线性回归模型，只要有观测值，就能估计出回归系数，得到经验回归方程。但是这个回归模型是否符合实际？应当做一系列检查，即回归诊断，才能保证回归模型符合实际。回归诊断包括：线性关系的F检验、自变量显著性的t检验、残差检验、多重共线性分析、影响分析、异方差检验、自相关检验等。其中线性关系的F检验、自变量显著性的t检验已在8.1.3节中介绍，这儿介绍多重共线性分析，当共线性问题严重时，介绍用岭回归和主成分回归估计待定参数。共线性分析的目的是考察自变量，包括常数项，是否存在共线性问题，即某个自变量的观测值是其他自变量（包括常数项）观测值的线性组合，或近似地是它们的线性组合。

有关多重共线性分析和影响分析的详细理论可见韦博成［20］或Belsley D.A等人［1］的著作。

8.1.6.1　线性回归模型的共线性问题

在8.1.1节中已介绍过线性回归参数估计是通过使

最小而得到的。在一定条件下，式（8-1）的极小解可以用矩阵运算表示参数估计的公式。

设有因变量和自变量的n次观测值，如下所示：

令

分别称之为因变量向量、待定参数向量、回归设计矩阵（简称为设计矩阵），设计矩阵是由自变量的观测值加上一列“1”形成的。理论上容易证明：只要X′X的行列式不为0，β的估计值可由

得到。但是从线性代数可知，当设计矩阵X的秩小于m+1时，也就是说设计矩阵X不满秩时，X′X的行列式为0，从而（X′X）-1不存在。然而式（8-1）的极小值仍是唯一的，而由最小二乘法求出的β的估计值不唯一。这时称回归模型具有完全多重共线性问题。由于“矩阵X不满秩”等价于“某个自变量的观测值是其余的一些自变量的线性组合加上常数”，所以当某个自变量的观测值等于其余自变量的线性组合加上常数时，这样的回归模型称为具有完全多重共线性，简称为具有完全共线性。具有完全共线性的模型可以设法求出全体解，但是这时模型的解会出现问题，和后文例8.7中的具有高度共线性问题不完全一样。

例8.6　设有回归模型

若其观测值如表8-8所示，则回归模型的设计矩阵是其中，第3列是第1列与第2列之和的2倍，或者说x2的观测值等于x1的观测值的2倍加2，所以模型具有完全共线性。

表8-8　具有完全共线性问题的数据

如果使用如下SAS代码作回归：

则提交程序后，输出结果中有如下一段：

这说明模型不满秩（not full rank），严格说来是设计矩阵不满秩，也就是模型具有完全共线性，即x1、x2和截距间存在关系：x2=2＊截距+2＊x1。从而使得最小二乘估计解不唯一，因而有诸多麻烦。这儿不解释整个输出的含义，而是另想办法建立模型（例如采用在8.1.6.3节和8.1.6.4节中介绍的方法）。每当回归模型具有完全共线性问题（某个自变量是一些自变量的线性组合与常数的和），在调用SAS的reg过程时，SAS都类似地输出上述的内容。

当某个自变量的观测值近似于其余自变量的线性组合加上常数时，这样的回归模型称为具有高度多重共线性问题，简称为具有高度共线性问题。具有高度共线性问题的回归模型不宜像8.1.2节那样调用reg过程计算和分析。

以下是一个具有高度共线性问题的回归模型的例子。

例8.7　设有回归模型

若其观测值如表8.9所示，则x2的观测值近似等于x1的观测值加2，所以模型具有高度共线性问题。

表8-9　具有高度共线问题的数据

如果使用如下SAS代码作回归：

则提交程序后得到的参数估计表是：

Parameter Estimates

由表可见变量截距、x1和x2的标准误差分别为53.85801，26.93837，26.93565，很大。

具有共线性问题的模型有很多缺点，例如估计出的参数不稳定（观测值发生微小的变动，估计出的参数就有较大的变动，不能正确反映自变量对响应变量的影响，而且估计量的方差很大）。详见吴诚鸥等人所编著的《近代实用多元统计分析》一书的第4章。

实际问题中，偶尔会遇到具有完全共线性的模型，如例8.5的数据不作逐步回归（见练习题），可以看出模型就具有完全共线性。这时SAS会像例8.6那样输出一段文字，告诉用户模型不满秩（not full rank）。实际问题中经常会遇到具有高度共线性的模型。怎样发现模型具有完全共线性或高度共线性问题？本书将在8.1.6.2节中予以介绍。如果模型具有高度共线性问题，怎样建立新型回归模型以避免这些缺陷？本书将在8.1.6.2—8.1.6.4节中予以介绍。

练习题　对于例8.5的数据，调用reg过程作二次回归，不筛选因子，结果如何？

8.1.6.2　用reg过程判断线性回归模型是否具有高度共线性问题

判断线性回归模型是否具有高度多重共线性问题称为多重共线性诊断。作多重共线性诊断的统计量有好几类，本书介绍的多重共线性诊断通过计算两类统计量来实现：最大条件指数（condition index）和方差比例（variance proportion）。完全多重共线性可以直接像例8.6那样，在调用reg过程时作多重共线性诊断，而在查看这两类统计量时也能发现共线性。

什么是最大条件指数？首先把矩阵X′X标准化：构造矩阵A，使A对角线上的元素等于X′X对角线上的元素，矩阵A其余元素为零。B=A-1／2 X′XA-1／2称为标准化的X′X。若标准化的X′X有r个特征值近似于零，则预报因子中有r个近似共线性关系。为了考察特征值是否为零，计算最大特征值与每个特征值之比：特征值与最小特征值之比的平方根称为条件指数，条件指数中最大值称为最大条件指数。当最大条件指数k很大时，认为有高度共线性问题。估计多重共线性问题的经验法则是：1≤k≤10预示自变量间有较弱多重共线性问题；10＜k≤100预示自变量间存在较强多重共线性问题；100＜k预示自变量间存在高度多重共线性问题。

当最大条件指数很大时，方差比例可以用来发现哪些自变量间近似存在相关性。什么是方差比例？方差比例和主成分分析有关，由于目前未介绍主成分分析，此处不便介绍方差比例的含义，读者仅需记住：当最大条件指数很大时，若某个自变量的方差比例大于0.5，则该自变量的观测值很可能与别的自变量线性相关。

怎样通过reg过程得到最大条件指数和方差比例？reg过程的model语句中，在被列出的最后一个自变量后加选项collin（注意用“／”隔开自变量和选项，以表示collin是选项而不是自变量）。提交这样的程序，输出中可以得到共线性诊断（Collinearity Diagnostics）表，其中有两个部分给出条件指数和方差比例。条件指数出现在Condition Index列，该列下的数值逐渐增大，其中最后一行的值（最大值）即最大条件指数k。通常方差比例出现在表的后面几列，当k较大，从而存在高度共线性时，检查最后一行中各自变量的方差比例。如果方差比例大于0.5，那么相应的自变量就存在共线性问题。

例8.8　对于例8.7的数据作共线性诊断。

解　采用如下程序：

提交程序后得到的结果中有表头为“Collinearity Diagnostics（共线性诊断）”的数表。

CoIIinearity Diagnostics

查看表中Condition Index（条件指数）列的最后一行，得到最大条件指数k=5501.74463，远大于100，可以判断自变量间存在高度多重共线性问题。截距（Intercept）和x1、x2的方差比例（Proportion of Variation）分别为0.99999、1、1都大于0.5，所以x1、x2和常数项间存在高度近似共线性问题。

例8.9　对于表8-8的数据采用reg过程作共线性诊断。

解　采用如下程序：

得到的主要诊断结果是：

CoIIinearity Diagnostics

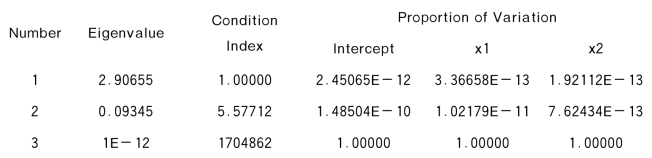
NOTE：SinguIarities or near singuIarities caused grossIy Iarge variance caIcuIations.To provide diagnostics，eigenvaIues are infIated to a minimum of 1e-12.

由于条件数k=1704862，可见共线性高度显著，膨胀因子都是1，显示x1、x2和截距间高度（完全）线性相关。所以具有完全共线性的模型也能被诊断存在严重共线性问题。

例8.8和例8.9所引用的数据都是人造的，以下介绍一个实例。

例8.10　某健身房统计31个人的跑步运动状况，包括：年龄、体重、氧气摄取率（Oxygen intake rate）、1.5英里跑步时间、不运动时脉搏、跑步时脉搏、跑步时最大脉搏共7项指标，得数据如表8-10所示。以氧气摄取率（单位为每分钟每公斤摄取毫升数）为因变量，其余变量为自变量，用reg过程建立线性回归模型并作共线性分析。(www.xing528.com)

表8-10　跑步者运动状况数据

解　分别以age、weight、oxy、runtime、rstpulse、runpulse、maxpulse表示年龄、体重、氧气摄取率、1.5英里跑步时间、不运动时脉搏、跑步时脉搏、跑步时最大脉搏，建立数据集fitness。调用reg过程，以oxy为因变量，其余变量为自变量，建立线性回归模型并作共线性分析。采用SAS如下程序：

提交上述程序后，得到有关共线性分析的表：

CoIIinearity Diagnostics

以上是共线性诊断表（为了便于印刷，方差比例的值四舍五入到万分位），其中有条件指数列（第3列）和方差比例列（最后7列）；由第3列可见最大条件指数196.78大于100，因而存在高度多重共线性。196.78所在行的方差比例中有两个（0.9128，0.9836）大于50%，因而它们对应的runpulse和maxpulse是相关的。这很符合实际：跑步时脉搏和跑步时最大脉搏应当相差不多。

注意：一般实际问题中，只有最后一行的条件指数（最大的条件指数）很大，倒数第二行的条件指数（第二大的条件指数）以及倒数第三行中的条件指数（第三大的条件指数）都不太大，这时只要在最后一行查找方差比例，看它是否大于0.5就能看出哪些自变量高度近似相关。如果最后几行有多个条件指数很大，这时应当把这几行的方差比例相加，若某个自变量的方差比例之和大于0.5，那么这个自变量就存在高度多重共线性问题。由于一时找不到像这样多个条件指数很大的高度近似的实例，此处以例8.5（完全共线性的例子）的数据作二次回归并作共线性分析。能看到有多个条件指数很大的情况，从而说明多个条件指数很大时，用方差比例之和查找自变量共线性的情况。采用下列程序（如果提交程序前数据集npk未建立，要像例8.5那样建立SAS数据集npk）：

提交后得到的输出中，关心的数据如下表：

由表中可见条件指数列最后3行的值都是2952462，都大于100，说明多重共线性很严重。检查其余列的最后3行，除n、p、k这3列外，所有数都不大于0.5。但是截距列最后3行之和即0.323310+0.336930+0.339770大于0.5；n列最后3行之和即1+0+0大于0.5；p列最后3行之和即0.000088+0.000016+0.999900大于0.5；k列最后3行之和即0.000092+0.999910+0大于0.5；np列最后3行之和即0.330110+0.336220+0.333670大于0.5；nk列最后3行之和即0.329940+0.336310+0.333750大于0.5；pk列最后3行之和即0.340230+0.328500+0.331270大于0.5。由此可见：变量截距、n、p、k、np、nk、pk之间存在高度相关性。

练习题　对表8-12的数据作共线性分析。

8.1.6.3　岭回归模型解决多重共线性的方法

当自变量间存在多重共线性时，常采取以下方法处理多重共线性。

（1）剔除不重要的自变量。如例8.10中跑步时脉搏runpulse与跑步时最大脉搏maxpulse紧密相关，则可剔除maxpulse，再作回归时多重共线性就减轻了。

（2）有时不想舍去预报因子，因为可能理论上或经验上这些预报因子都对于因变量有较大影响，舍去这些预报因子不合理，这时可用两个方法：①用原有数据拟合岭回归模型；②用原有数据的主成分拟合回归模型。这儿先介绍岭回归模型。

岭回归模型的原理是：多重共线性使|X′X|等于零或近似于零，从而由参数估计公式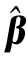=（X′X）-1 X′Y造成方差过大，此时可以选定一个岭常数（ridge constant）c。改用参数的岭估计公式（c）=（X′X+cI）-1 X′Y，其中c是（0，1）中的某个值，岭估计的英文是ridge regression estimates。理论上可以证明虽然岭估计是有偏估计，但是参数β的岭估计误差的方差变小，从而使稳定性大大提高了。

确定岭常数c的原理是：在（0，1）中选取不同的数进行尝试，分别取这些数为岭参数，计算岭估计，看看哪个效果好，选取效果最好的作为岭常数c。效果好的原则是：c尽可能小，同时c的变化对岭回归系数的影响不大。为此要多在0附近选些数，离0稍远的地方少选些数，检查c取作这些数时岭估计变化的情况。

实现岭回归模型的SAS做法是：在proc reg语句中加选项“ridge=”，该选项等号后给出的值就是设定的岭常数；再在语句中加选项“outest=文件名”，用于指定在文件中存储输出的岭估计值；然后在model语句后增加语句“plot／ridgeplot；”，该语句指示SAS画出岭常数c取不同值时，岭估计的折线图；最后输出选项“outest=”所指定的文件，在该文件中找出合适的岭估计。

例8.11　某国连续11年的进口总额（import）、国民生产总值（GDP）、总储蓄量（save）、总消费量（cosume）数据如表8-11所示，试建立由国民生产总值、总储蓄量、总消费量预测进口总额的经验公式。

表8-11　某国连续11年的经济数据

解　建立回归模型如下：

用SAS的reg过程估计参数，得经验回归方程为：

其中，GDP系数为负数，这与实际情况不符。实际情况中，GDP增大，进口总额应当增大。GDP系数为负数却导致相反结果：GDP增大了进口总额反而减少了。怀疑造成此情况的原因是共线性存在。为此作共线性诊断，采用如下程序：

提交程序后所得输出中有如下诊断表：

CoIIinearity Diagnostics

表中最后一行指出最大条件指数265.46126远大于100，说明存在高度共线性；最后一行中还查出GDP和consume的方差比例大于0.5，说明它们存在相关性。如果从自变量GDP和consume中删去一个：改用自变量GDP和save建立预测import的回归模型，那么就不存在高度共线性了（最大条件指数仅为16.54）；或用consume和save建立预测import的回归模型，也不存在共线性了（最大条件指数仅为17.22）。但是变量GDP和save都对于预测import有较大作用，删去任何一个都不好。为此想到以GDP、consume和save为自变量作岭回归。为了作岭回归，想使c尽可能小，考虑在0和0.1间每隔0.01选1个岭常数，0.2和0.5间每隔0.1选一个岭常数，对于这14个岭常数分别作出岭估计并画出连线图。采用如下程序：

提交程序后得到图8-3和岭估计表。

图8-3　进口量岭估计图

岭估计表

从图8-3中可见岭参数值大于0.02后几条曲线都平稳变化，于是取岭参数为0.02。岭估计表中＿ridge＿所在列是岭常数列，查找其中岭常数值为0.02的行，即第4行，其中b0，b1，b2，b3的估计值分别为b0=-8.9277，b1=0.057343，b2=0.59542，b3=0.12663。所以经验岭回归方程就是

理论上可以证明岭回归不具有无偏性，本例中GDP、consume和save的系数的估计值不具有无偏性。

练习题　已知自变量x1、x2和因变量y的观测值如表8-12所示，使用岭回归估计参数。

表8-12　自变量x1、x2和因变量y的观测值

8.1.6.4　主成分回归

解决共线性问题的另一办法是主成分回归：由m个自变量数据选出前q个主成分（q＜m），主成分间是互不相关的；再保持因变量不变，用这q个主成分作为自变量作回归；最后把所得回归结果作变量代换，转化成原来因变量与原来自变量的关系。因为目前还没有介绍主成分概念，细节就不介绍了，关心的读者们可以参考吴诚鸥等人著作［21］的第5章。

用sas-reg过程实现主成分回归的步骤是：在proc reg语句中加选项“outest=文件名”（存储主成分回归的输出数据集）；在model语句的自变量后加“／”，再加选项“pcomit=k”（k为略去的主成分个数k=m-q）。提交后看输出结果中最后一张表的最后一行即可。

例8.12　某国连续16年民航客运量y（万人）、国民收入x1（亿元）、消费额x2（亿元）、铁路客运量x3（万人）、民航航线里程数x4（万公里）、来华旅游人数x5（万人）如表8-13所示。试建立以民航客运量为因变量，以x1—x5为自变量的回归方程。

表8-13　某国民航数据表

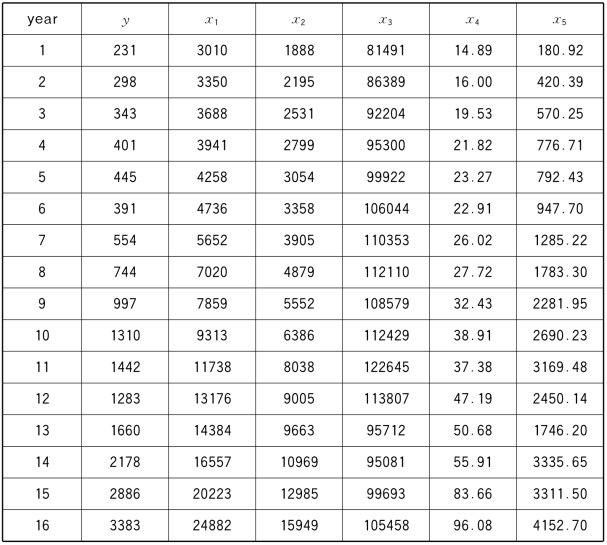
解　直接用reg过程建立回归方程发现，经验回归方程消费额x2的系数是负的，这与实际情况不符：消费额越多，应当乘飞机人数越多；而回归方程x2的系数是负的，导出错误结论：消费额越多，则乘飞机人数越少。通过检验发现，x2的系数是负的原因是：回归模型出现多重共线性（最大条件指数等于257.31），查看方差比例可以看出x1和x2高度相关。和例8.11一样，仍希望建立用这5个自变量预测乘飞机人数的线性回归模型，为此可以考虑主成分回归。本例中自变量有5个，主成分也有5个。通过主成分分析，发现前3个主成分累计百分比为99.61%，即包含5个自变量的99.61%的信息，因此选用前3个主成分，去掉2个主成分，仍然可以保留全部自变量的99.61%的信息。于是可用如下SAS程序计算：

提交后输出的最后一张表为（注意：表中共有3行，第1行英文字符竖排，是因为变量太多之故，它们的顺序是Obs＿MODER＿，＿TYPE＿，＿DEPVAR＿（因变量），＿RIDGE＿，＿PCOMET＿（删去主成分个数），＿RMSE＿，Intercep（截距），x1，x2，y3，x4，x5，Y）：

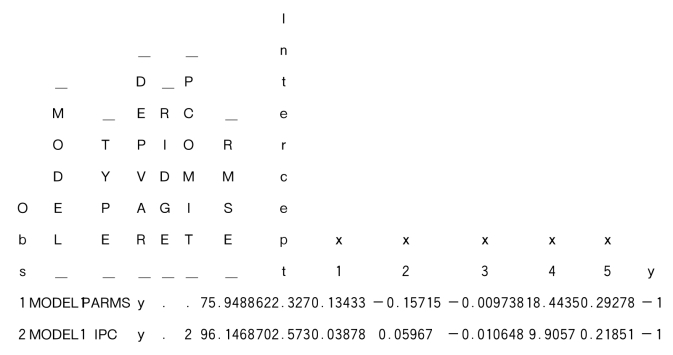
该表倒数第二行和最后一行分别是：不减少主成分和减少两个主成分所得的参数估计，我们只关心其中最后一行，而且只关心其中回归系数。由该表最后一行可见主成分法得到的回归方程就是：

其中，消费额x2的系数就是正的了。

目前没有介绍主成分，读者可以参考有关书籍学习主成分分析。因为未学过主成分分析时不能决定选几个主成分，未学过主成分分析的读者可以采用另一种方法，决定删去主成分的个数：可以先选pcomit=1（去掉1个主成分）作一次主成分回归，看看所得经验回归方程的效果好不好，如果效果不好再令pcomit=2（去掉2个主成分），乃至pcomit=3（去掉3个主成分）……直到选得合适的经验回归方程为止。

理论上可以证明主成分回归不具有无偏性，本例中x1—x5的系数的估计值不具有无偏性。

练习题　对于例8.11的数据作主成分回归，k=1。应与岭回归结果差不多。