社会特征变异性研究：科学方法在社会生活中的应用

另一个估计样本大小的重要因素，是研究特征（变量）的变异程度，变异小，小的样本便足够。比如，若有99%的中学生数学及格，随机抽样出来的样本即使很小，偏差也不会大到哪里去。变异的两种情况若是九一分，样本可小些；若是七三分，要大一些；在五五分时，样本要最大，这是最容易搞错的地方。表9-3是在表9-2的基础上，加上特征变异性的考虑后对样本大小的要求。

表9-3　95%可靠度下特征变异和样本大小的关系*

*假设了样本是经过简单随机法抽出来的。
@样本太小，分析会失去意义。
Source：D.A.deVaus，Surveys in Social Research，London：George Allen&Unwin，1986，p.64.

引用这个表前须解决两个问题。第一个，未抽出样本时如何知道特征的变异程度。一个做法是根据以往的或类似的经验，估计研究特征的大约变异程度。这当然危险，估计如果相距太远，分析时发现样本太小，推论的打算便落空。如果没有任何经验可用，那么另一个做法是先抽一个很小的样本，但风险依然很大。稳健起见，应该把变异程度估计得大些，最大的当然是五五分了。

须解决的第二个问题是：每次搜集资料时，我们很少会局限于一个特征，数学及格率的变异可能是八二分，语文优秀率的可能是一九分，家长直接帮助的可能是三七分……求稳健计，宜以变异较大的特征为准。

这里有一套粗略的样本计算尺（图9-1），把两种可靠度（95%、99.7%）下的准确度、特征变异比和样本大小四者间的关系，一目了然地表达出来。图内三柱，左柱是变异是否比，中柱是样本大小，右柱左边是95%可靠度下的偏差百分率，右边是99.7%可靠度下的偏差百分率^[2]。决定了任何两柱上的数值后，用直尺连接起来，直尺与第三柱的交接点，便是第三者的数值。例如想估计中学生数学及格率，你若决定接受95%的可靠度和上浮不超过2.5%的偏差百分率，且去年报告显示有20%不及格，为稳健起见，把变异比估作三七分，图尺立即告诉你样本应该有1250左右。如果主办人说，研究经费不足，请把样本缩小至1000，你须先估计这个样本数下偏差率会提高多少，根据样本计算尺，变异三七分、样本1000、95%可靠度，偏差率会上升至大约2.8%，这是双方都能够容忍的推论吗？

根据图9-1、表9-2和表9-3得到的是粗略的估计值，希望准确计算四者关系的读者，可以采用以下公式。

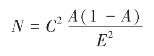(www.xing528.com)

其中　N——样本大小；

C——可靠度的标准偏差数，90%时C=1.65，95%时C=1.96，99%时C=2.58，99.7%时C=3；

A——特征变异百分率，如若是30%，则A（1-A）=30×70=2100；

E——偏差百分率。

图9-1　粗略样本计算尺

如果你对变异比毫无认识，那么最稳妥的估计是一半对一半，A（1-A）=50×50=2500。你希望估计结果的准确程度达±2.5%之内，E2=2.52=6.25；你也希望可靠性达99.7%，99.7%可靠度的标准偏差数是3，C2=32=9，那么，你需要的样本=（9×2500）/6.25=3600。

这个样本带来的准确度和可靠度很高，但成本也很高。如果愿意接受95%的可靠度，你需要的样本会降至1536［（1.962×2500）/2.52≈1536］。如果又愿意接受95%的准确度，你需要的样本会降至384［（1.962×2500）/52≈384］。如果愿意接受三七分的变异性，你需要的样本会降至323［（1.962×30×70）/52≈323］。